Two buses travel between Jamshedpur and Kolkata in the opposite directions, on the same road. On that road, the maximum allowed speeds are different (but constant) for the opposite directions. Usually, both buses travel at the respective maximum allowed speeds to their respective destinations: the bus from Jamshedpur to Kolkata takes 4 hours, while the bus from Kolkata to Jamshedpur takes 3 hours.
One day, the two buses start at the same time. However, one hour after starting, the bus from Jamshedpur to Kolkata reduces its speed to half of its maximum allowed speed due to congestion on the road.
If both buses do not stop anywhere in between, how many hours after starting do they meet?

Let the maximum allowed speed from Jamshedpur to Kolkata be s1 kmph and the maximum allowed speed from Kolkata to Jamshedpur be s2 kmph. Since the bus is moving at the maximum allowed speed then we can say that the speed of the bus moving from Jamshedpur to Kolkata (Bus 1) is s1 kmph and the speed of the bus moving from Kolkata to Jamshedpur (Bus 2) is s2 kmph.

Time taken by Bus 1 to travel from Jamshedpur to Kolkata = 4 hrs

Distance travelled by Bus 1 = 4 $$\times\ $$s1

Time taken by Bus 2 to travel from Kolkata to Jamshedpur = 3 hrs

Distance travelled by Bus 1 = 3 $$\times\ $$s2

Since both the bus is travelling on the same road, the distance travelled by both the buses will be same. 

4 $$\times\ $$s1 = 3 $$\times\ $$s2

$$\ \frac{\ s1}{s2}=\ \frac{\ 3}{4}$$

The ratio of speed of Bus 1 to the speed of Bus 2 is 3:4.

Hence, let the speed of Bus 1 be 3x kmph and the speed of Bus 2 be 4x kmph.

Total distance travelled by the buses = $$4\times\ 3x\ =3\times\ 4x=12x$$

Now, both the buses started at the same time and travelled at the maximum allowed speed for 1 hr. 

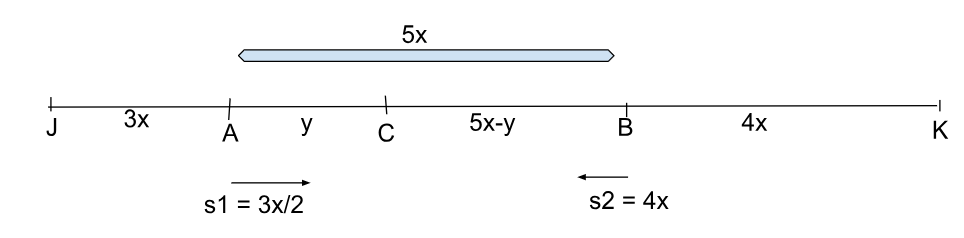
Distance travelled by Bus 1= JA = $$3x\times\ 1=3x$$

Distance travelled by Bus 2= KB = $$4x\times\ 1=4x$$

Distance left to be travelled= AB = $$12x-\left(3x+4x\right)=5x$$

Now, the speed of Bus 1 is reduced to half due to congestion. 

New speed of Bus 1 = $$\ \frac{\ 3x}{2}$$

After the reduction of speed, let the two buses meet at point C and the time taken by both the buses to reach C is the same. 

Let the distance travelled by Bus 1 from A to C be y km. 

BC = 5x-y km

Hence, $$\ \frac{\ y}{\ \frac{\ 3x}{2}}=\ \frac{\ 5x-y}{4x}$$

y = $$\ \frac{\ 15x}{11}$$

Time required = $$\ \frac{\ \ \frac{\ 15x}{11}}{\ \frac{\ 3x}{2}}=\ \frac{\ 10}{11}$$ hrs

Total time required for both the buses to meet = $$\frac{\ 10}{11}+1=\ \frac{\ 21}{11}$$ hrs

Hence, both the buses will meet after $$\frac{\ 21}{11}$$ hrs from starting. 

$$\therefore\ $$ The required answer is D.