An archer, from the point A, is aiming at a target, placed on the top of a 56 feet tall tree. The base of the tree is at the point C. From the archer’s position, the angle of elevation to the target is 45° from his eye level. The archer, facing the tree, moves backwards on the straight line joining the points A and C, to a new position at the point B. From the point B, the angle of elevation from his eye level to the target becomes 30°.
How far did the archer move from A to B (in feet) if his eye level is at a height of 6 feet from the ground?

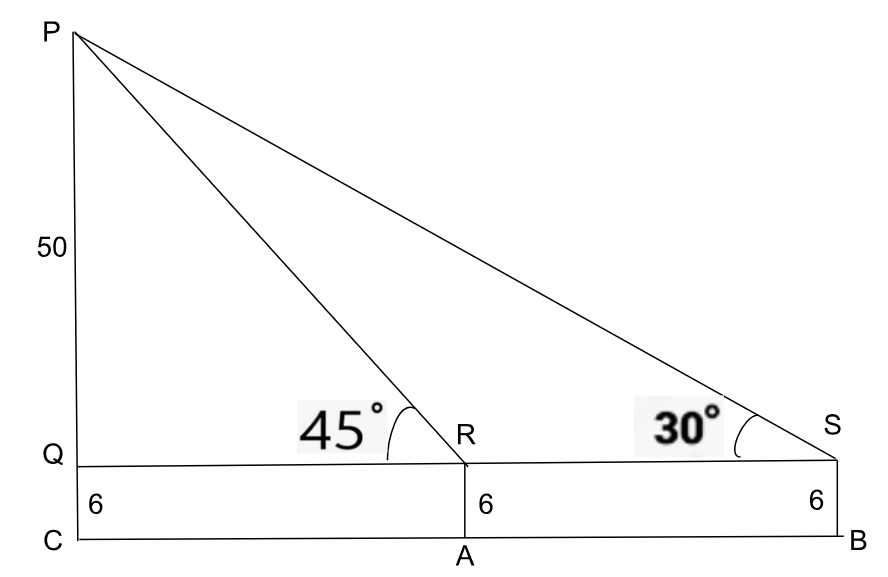
Let the tree be PC and the archer be RA. 

Given : Height of the tree = 56ft, height of the archer up to the eye level = 6ft, angle of elevation at point A = 45$$^{\circ\ }$$, angle of elevation at point B = 30$$^{\circ\ }$$  

To find : Length of AB

In $$\triangle\ $$PQR, $$\tan\ 45^{\circ\ }=\ \frac{\ PQ}{QR}=\ \frac{\ 50}{QR}$$

QR = 50ft (as $$\tan\ 45^{\circ\ }=\ 1$$)

Now, in $$\triangle\ PQS$$, 

$$\tan\ 30^{\circ\ }=\ \frac{\ PQ}{QS}=\ \frac{\ PQ}{QR+RS}=\ \frac{\ 50}{50+RS}$$

$$\ \frac{\ 1}{\sqrt{3\ }}=\frac{\ 50}{50+RS}$$

RS = $$50\left(\sqrt{3\ }-1\right)$$ ft

Since RS = AB, AB = $$50\left(\sqrt{3\ }-1\right)$$ ft

Hence, the length of AB is $$50\left(\sqrt{3\ }-1\right)$$ feet

$$\therefore\ $$ The required answer is C.