XAT 2026 Question Paper
For the following questions answer them individually
XAT 2026 - Question 11
Three categories of candidates appear for an admission test: diligent (10%), lazy (30%) and confused (60%). A diligent candidate is 10 times more likely to clear the admission test compared to a lazy candidate.
If 40% of the candidates clearing the admission test are confused, what is the MAXIMUM possible value of the probability of a confused candidate clearing the test?
XAT 2026 - Question 12
In a multiple-choice examination, there are 20 questions. Each correct answer is worth 4 marks, while 2 marks are to be deducted for every wrong answer. Further, 1 mark is to be deducted for every unattempted question. One student receives a total of 46 marks in the examination. However, before releasing the marks, the professor realizes that she has, by mistake, deducted 2 marks for every unattempted question and 1 mark for every wrong answer.
After correction, how many marks will the student get?
XAT 2026 - Question 13
Let $$f:R^{2}\rightarrow R$$ be a real-valued function defined as $$f\left(0, y\right)=y+1 \text{and} f\left(x+1, y\right)=f\left(x, f\left(x, y\right)\right)+ x$$. What is the value of $$f(2, 2)$$?
XAT 2026 - Question 14
Let $$a_{1}<a_{2}<.... <a_{n}$$ be the list of all prime numbers less than 25. Define $$X_{i}=\frac{b_{i}}{a_{i}}$$, where $$b_{i}$$ is the sum of all $$a_{k}$$ where k ranges from 1 to n, $$k \neq i$$. Let B be the set of all integer-valued $$X_{i}$$. What is the Smallest element of B?
XAT 2026 - Question 15
Consider two circles, each having radius of 5cm (centimeters), touching each other at a point P. A direct tangent QR is drawn touching one circle at a point Q and the other circle at a point R. Inside the region PQR inscribed by the two circles and the tangent, a square ABCD is inscribed with its base AB on the tangent and the other side touching the two circles at points D and C, respectively.
Find the area of the square ABCD.
XAT 2026 - Question 16
Rajan is a fruit seller. On any day, he sells only one kind of fruit. On the first day, he buys 9 kg of blueberries. On the second day, he buys 22 kg of kiwis. On the third day, he buys 50 kg of peaches. The per kg purchase price of each fruit is an integer. Further, on each of these three days, he spends the same amount to purchase fruits. On the fourth day, he buys mangoes at Rs. 35/kg and spends Rs. 15 less than any of the previous three days.
If he then sells all the mangoes at Rs. 50/kg, what is his MINIMUM possible profit on the fourth day?
XAT 2026 - Question 17
How many solutions $$\left(x, y, z\right)$$ of the equation $$x+y^{2}+z^{3}=50$$ exist, where x, y and z are positive integers?
XAT 2026 - Question 18
A triangular plot is such that two of its sides, of lengths 90m (meter) and 60m, are perpendicular to each other. There is a housing complex in a rectangular region within the plot. The area of the rectangular region is 4/9th of the area of the triangular plot. Additionally, two sides of the rectangular region lie on the two perpendicular sides of the triangle, and one vertex is on the hypotenuse. The members of the housing complex want to construct a wall along the perimeter of the rectangular region.
If the cost of construction is Rs. 5000/m, what is the MINIMUM possible cost of building the wall?
XAT 2026 - Question 19
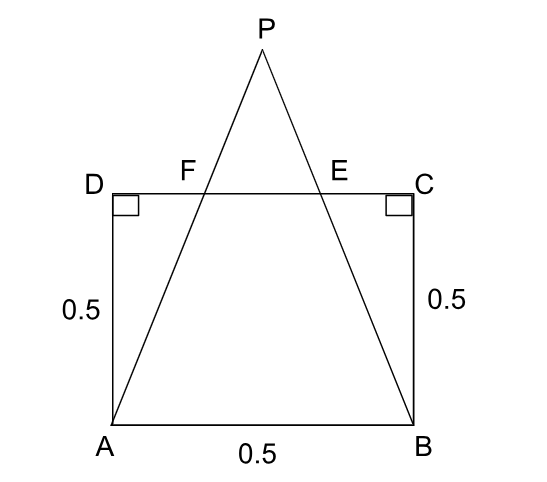
During Durga Puja, for the purpose of lighting, one puja pandal in Kolkata used many identical structures made of wooden sticks. The design of the structures was as follows: each structure was constructed with the help of six wooden sticks by combining an isosceles triangular structure, and a square structure, with the bases of both structures being the same. Let us take one such structure. Call the triangle PAB, with PA = PB, and the square ABCD, with AB being the same wooden stick as a common base for the triangle and the square. To make the structure strong, the two equal sides of the triangular structure were tied with the opposite side of square’s base, i.e., CD, at points E and F, in such a way that CE = EF = FD. The structure was hung from P.
If AB = 0.5m (meter), the total length of wooden sticks required for twenty such structures is:
XAT 2026 - Question 20
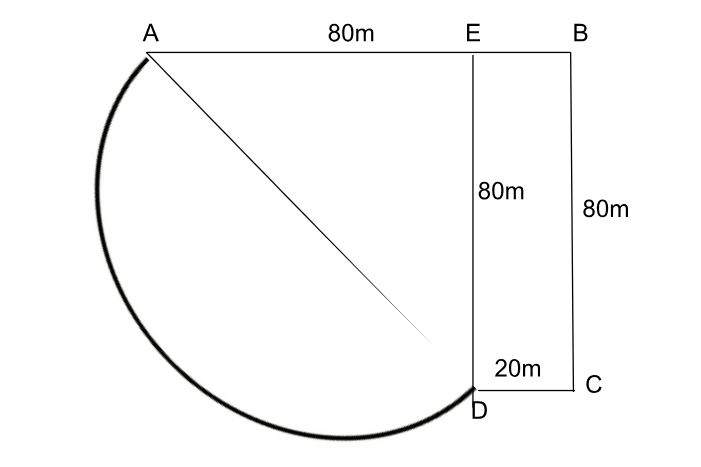
A park has two gates, Gate 1 and Gate 2. These two gates are connected via two alternate paths. If one takes the first path from Gate 1, they need to walk 80m (meters) towards east, then 80m towards south, and finally 20m towards west to arrive at Gate 2. The second path is a semi-circle connecting the two gates, where the diameter of the semi-circle is the straight-line distance between the two gates.
A person walking at a constant speed of 5 kilometers/hour enters the park through Gate 1, walks along the first path to reach Gate 2 and then takes the second path to come back to Gate 1.
Which of the following is the CLOSEST to the time the person takes, from entering the park to coming back to Gate 1, if she never stops in between?

.webp)