IIFT 2022 Slot 1 Question Paper (18th Dec)
For the following questions answer them individually
IIFT 2022 Slot 1 (18th Dec) - Question 11
Let integer $$\alpha$$ be one of the roots of $$ax^2 + 2x + 3 = 0$$ and integer $$\beta$$ be one of the roots of $$5x^2 + bx + 8 = 0$$. It is also given that $$\alpha = \beta^2$$. Which of the following statement is true if $$b = -14$$?
IIFT 2022 Slot 1 (18th Dec) - Question 12
Find the value of x such that
$$(1 - x)^{\frac{3}{2}} + (1 + x)^{\frac{3}{2}} + 2(\sqrt{1 - x^2}) = (2 + 2\sqrt{1 - x^2})^{\frac{3}{2}}$$
IIFT 2022 Slot 1 (18th Dec) - Question 13
An integer is called a perfect square if it is square of another integer. The number of perfect square points (i.e. both coordinates are perfect squares that lie exactly within the circle
$$(x - 12)^2 + (y - 10)^2 = 64$$ is
IIFT 2022 Slot 1 (18th Dec) - Question 14
An n-digit number is a positive number with exactly n digits. Nine hundred distinct n-digit numbers are to be formed using digits 2,3,4,5 and 7 such that each n-digit number has the
(i) first and last digits are the same
(ii) first and third are prime numbers
(iii) second should be greater than or equal to 4.
What should be the minimum value of n such that the above is possible?
IIFT 2022 Slot 1 (18th Dec) - Question 15
Pot "A" contains 5 blue and 10 green balls, and another pot "B" contains 7 blue and 2 green balls. A biased dice with six sides numbered 1 to 6 is rolled. The probability of each odd outcome is the same, and the probability of each even outcome is the same. But the probability of an odd outcome is twice the probability of an even outcome. If the face 1 or 2 or 3 comes up, a ball is taken from the pot "A" else a ball is taken from the pot "B". Find the probability of drawing a green ball.
IIFT 2022 Slot 1 (18th Dec) - Question 16
In 1920, the "Sahitya Shakti" society was established by 500 members who read Premchand. In 1921, due to internal conflict, it removed all 200 members who also read Shakespeare. In 1922, further the member who also read Tolstoy numbering 100 left the society. In 1923, the society added only those ex-member who read both Shakespeare and Premchand but not Tolstoy after which the Sahitya Shakti society consisted of 350 members. Which of the following is true?
IIFT 2022 Slot 1 (18th Dec) - Question 17
It is given that $$P(A \cup B) < \frac{3}{4}, P(A) > \frac{1}{8}, P\left(\frac{A}{B}\right) < \frac{1}{2}$$. Which of the following is true?
IIFT 2022 Slot 1 (18th Dec) - Question 18
Find $$\tan^4 \alpha + \tan^4 \gamma$$ using the information given below:
$$\tan(\theta - \gamma) = \frac{1}{\sqrt{2}}, \tan \theta \tan \gamma = \tan^2 \alpha$$
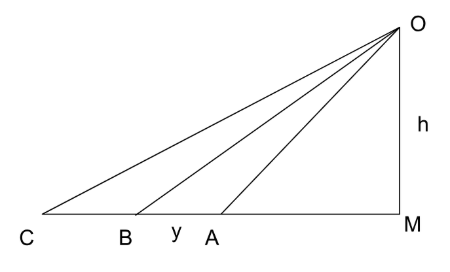
IIFT 2022 Slot 1 (18th Dec) - Question 19
A person standing on the bank of a river observes that the angle subtended by a tree on the opposite bank is 60 degrees. When he retires 'y' metre from the bank perpendicular to the tree, he finds the angle to be 45 degrees. When he further retires $$15 - 5\sqrt{3}$$ metre perpendicular to the tree, he finds the angle to be 30 degrees. Find the height of the tree in metres?
IIFT 2022 Slot 1 (18th Dec) - Question 20
Let a - d, a, a + d, a + 2d be four terms of an arithmetic progression with integer entries and a, a + d, a + 2d, a + 3d be another four terms of the same arithmetic progression. Let $$x = a(a - d) (a + d) (a + 2d) + d^4$$ and $$y = a(a + d) (a + 2d) (a + 3d) + d^4$$. Then x + y is equal to ?