In a parallelogram ABCD of area 72 sq cm, the sides CD and AD have lengths 9 cm and 16 cm, respectively. Let P be a point on CD such that AP is perpendicular to CD. Then the area, in sq cm, of triangle APD is

In a parallelogram ABCD of area 72 sq cm, the sides CD and AD have lengths 9 cm and 16 cm, respectively. Let P be a point on CD such that AP is perpendicular to CD. Then the area, in sq cm, of triangle APD is

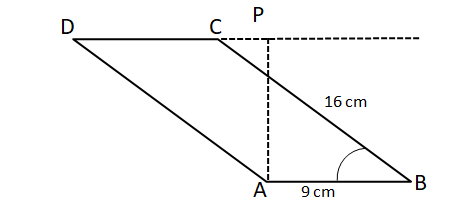
Given that area of parallelogram = 72 sq cm

Area of triangle ABC = $$\dfrac{1}{2}$$*area of parallelogram

(1/2)*AB*BC*sinABC = $$\dfrac{1}{2}$$*72

sinABC = $$\dfrac{1}{2}$$

$$\angle$$ ABC = 30°

Let us draw a perpendicular CQ from C to AB. 

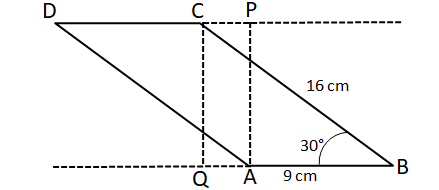
$$\angle\ B\ =\ \angle\ D\ =\ 30^{\circ\ }$$ ( opposite angles in a parallelogram)

$$\angle\ QCB\ =\ \angle\ DAP\ =\ 60^{\circ\ }$$  ( Sum of angles in a triangle = 180)

In triangles APD and CQB, AP= CQ , AD=CB ( opposite sides of a parallelogram) , $$\angle\ QCB\ =\ \angle\ DAP\ =\ 60^{\circ\ }$$

Hence APD and CQB are congruent triangles using SAS property.

Therefore, we can say that area of triangle APD = area of triangle CQB

In right angle triangle CQB,

QB = CBcos30° = $$16*\dfrac{\sqrt{3}}{2}$$ = $$8\sqrt{3}$$ cm

CQ = CBsin30° = $$16*\dfrac{1}{2}$$ = $$8$$ cm

Therefore, area of triangle CQB = 1/2*CQ*QB = $$1/2*8*8\sqrt{3}$$ = $$32\sqrt{3}$$

Hence, we can say that area of triangle APD = $$32\sqrt{3}$$.