Please enter the following details
Comprehension:
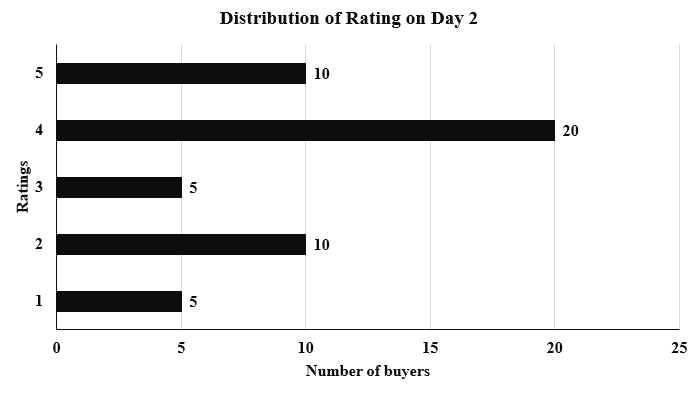
An online e-commerce firm receives daily integer product ratings from 1 through 5 given by buyers. The daily average is the average of the ratings given on that day. The cumulative average is the average of all ratings given on or before that day. The rating system began on Day 1, and the cumulative averages were 3 and 3.1 at the end of Day 1 and Day 2, respectively. The distribution of ratings on Day 2 is given in the figure below.
The following information is known about ratings on Day 3.
1. 100 buyers gave product ratings on Day 3.
2. The modes of the product ratings were 4 and 5.
3. The numbers of buyers giving each product rating are non-zero multiples of 10.
4. The same number of buyers gave product ratings of 1 and 2, and that number is half the number of buyers who gave a rating of 3.
We are given that on day 3, a total of 100 ratings came in
The modes were 4 and 5, meaning that an equal number of 4 and 5 ratings came in; let it be 10b (since we are given that all ratings were non-zero multiples of 10)
Let's take the number of 1 and 2 ratings as 10a each, giving the number of 3 ratings as 20a
Adding all of these up: 10a+10a+20a+10b+10b = 100
40a+20b = 100
2a+b = 5
The only integer combination for a and b, without them being zero, is a being 1 and b being 3 or a=2 and b=1
But taking b as 1 would make 3 as the mode rating, so we can not consider the latter case.
We are giving 10 - 1 ratings, 10 - 2 ratings, 20 - 3 ratings, 30 - 4 ratings, and 30 - 5 ratings.
The average would be $$\frac{\left(10\times\ 1\right)+\left(10\times\ 2\right)+\left(20\times\ 3\right)+\left(30\times\ 4\right)+\left(30\times\ 5\right)}{100}=\frac{360}{100}=3.6$$
Therefore, Option A is the correct answer.
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 38+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free
