Please enter the following details
Comprehension:
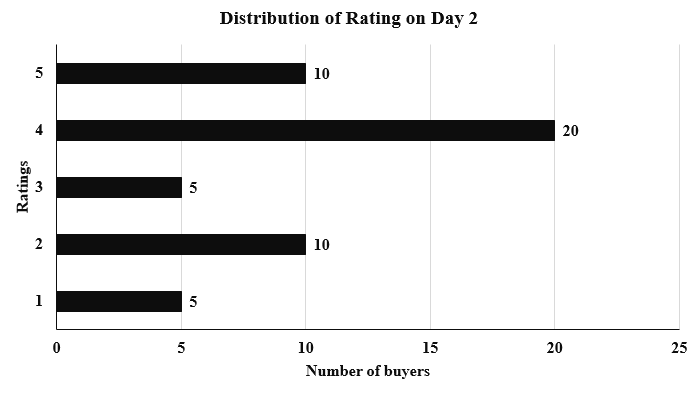
An online e-commerce firm receives daily integer product ratings from 1 through 5 given by buyers. The daily average is the average of the ratings given on that day. The cumulative average is the average of all ratings given on or before that day. The rating system began on Day 1, and the cumulative averages were 3 and 3.1 at the end of Day 1 and Day 2, respectively. The distribution of ratings on Day 2 is given in the figure below.
The following information is known about ratings on Day 3.
1. 100 buyers gave product ratings on Day 3.
2. The modes of the product ratings were 4 and 5.
3. The numbers of buyers giving each product rating are non-zero multiples of 10.
4. The same number of buyers gave product ratings of 1 and 2, and that number is half the number of buyers who gave a rating of 3.
From the given chart, we can find the average rating on day 2:
$$\frac{\left(5\times\ 1\right)+\left(10\times\ 2\right)+\left(5\times\ 3\right)+\left(20\times\ 4\right)+\left(10\times\ 5\right)}{5+10+5+20+10}=\frac{170}{50}=3.4$$
We are given the cumulative average of day 1 and day 2 as 3.1, and the average at the end of day 1 is 3.
Let's take the number of ratings received on day 1 as $$x$$; using this overall average and the average on day 2, we get the equation:
$$\frac{3x+\left(50\times\ 3.4\right)}{x+50}=3.1$$
$$3x+170=3.1x+155$$
$$15\ =\ 0.1x$$
$$x=150$$
Therefore, the number of ratings received on day 1 is 150.
Create a FREE account and get:
- All Quant CAT complete Formulas and shortcuts PDF
- 38+ CAT previous year papers with video solutions PDF
- 5000+ Topic-wise Previous year CAT Solved Questions for Free
