A park has two gates, Gate 1 and Gate 2. These two gates are connected via two alternate paths. If one takes the first path from Gate 1, they need to walk 80m (meters) towards east, then 80m towards south, and finally 20m towards west to arrive at Gate 2. The second path is a semi-circle connecting the two gates, where the diameter of the semi-circle is the straight-line distance between the two gates.
A person walking at a constant speed of 5 kilometers/hour enters the park through Gate 1, walks along the first path to reach Gate 2 and then takes the second path to come back to Gate 1.
Which of the following is the CLOSEST to the time the person takes, from entering the park to coming back to Gate 1, if she never stops in between?

The figure of the path is given below. Gate 1 and Gate 2 is situated at A and B respectively. 

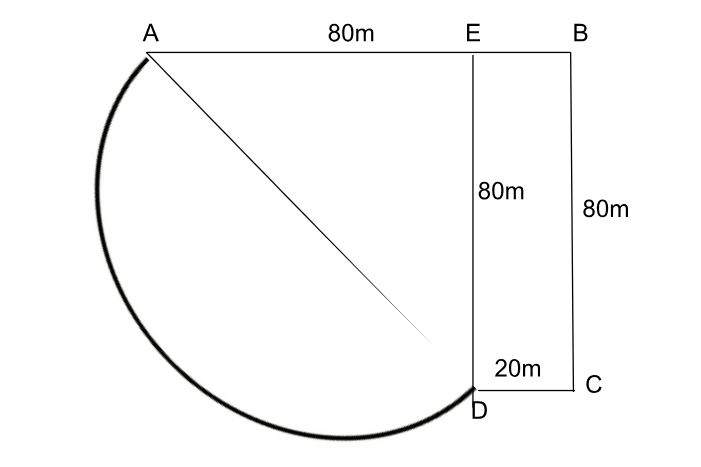
We have drawn ED which is perpendicular to AB in order to get a right angled triangle AED where AE = 60m and ED = 80m. 

From pythagoras theorem, $$AD^2=AE^2+ED^2$$

$$AD^2=60^2+80^2$$

AD = 100m

Length of the semi circular path AD = $$\pi\ r=\pi\ \left(\frac{AD\ }{2}\right)\ $$ = $$50\pi\ \ $$ = 157 m

Length of path ABCD = 80+80+20 = 180 m

A person entered through gate 1 and travelled along path 1 and path 2 and exited from gate 1. 

Total distance covered = 180+157 = 337m

Speed of the person = 5 kmph = $$\ \frac{\ 5\times\ 1000}{60}=\ \frac{\ 250}{3}\ \frac{\ m}{\min}$$

Total time taken = $$\ \frac{\ 337}{\ \frac{\ 250}{3}}\min$$ = 4 min (approx)

So the total time taken for the person to travel across the park is 4 min. 

$$\therefore\ $$ The required answer is A.