During Durga Puja, for the purpose of lighting, one puja pandal in Kolkata used many identical structures made of wooden sticks. The design of the structures was as follows: each structure was constructed with the help of six wooden sticks by combining an isosceles triangular structure, and a square structure, with the bases of both structures being the same. Let us take one such structure. Call the triangle PAB, with PA = PB, and the square ABCD, with AB being the same wooden stick as a common base for the triangle and the square. To make the structure strong, the two equal sides of the triangular structure were tied with the opposite side of square’s base, i.e., CD, at points E and F, in such a way that CE = EF = FD. The structure was hung from P.
If AB = 0.5m (meter), the total length of wooden sticks required for twenty such structures is:

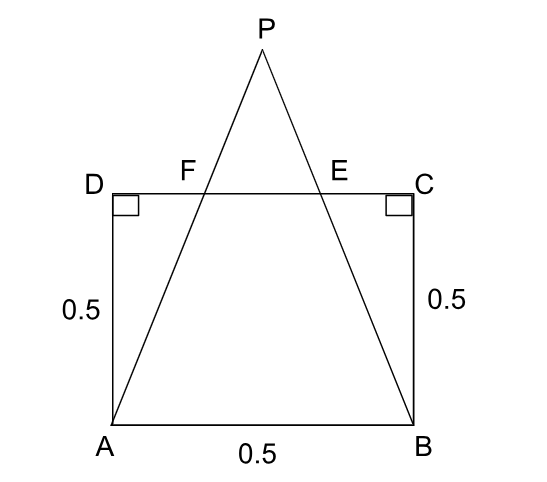
The figure of one of the structure is given above. 

Since, ABCD is a square, AB = CD = 0.5 m

Now, CE=EF=DF= (Given) = CD/3 = $$\ \ \ \frac{\ 0.5}{3}=\ \frac{\ 1}{6}m$$

Let PE = x m and EB = y m respectively. 

In $$\triangle\ $$PFE and $$\triangle\ $$PAB, 

$$\angle\ P=\angle\ P$$ (common angle)

$$\angle\ PFE=\angle\ PAB$$ (since FE is parallel to AB)

Hence, $$\triangle\ $$PFE and $$\triangle\ $$PAB are similar. 

$$\ \frac{\ PE}{PB}=\ \frac{\ FE}{AB}$$

$$\ \frac{\ PE}{PE+EB}=\ \frac{\ FE}{AB}$$

$$\ \ \ \frac{\ x}{x+y}=\ \frac{\ \ \frac{\ 1}{6}}{0.5}$$

y = 2x i.e. EB = 2 $$\times\ $$PE

Now, in $$\triangle\ $$ECB, 

$$EB^2=EC^2+CB^2$$

$$\left(2x\right)^2=\ \left(\frac{1\ }{6}\right)^2+\ \left(\frac{1\ }{2}\right)^2$$

$$x=\ \frac{\ \sqrt{10\ }}{12}m$$

PB = PE + EB = x + 2x = 3x = $$\ \frac{\ \sqrt{10}}{4}\ $$m

Length of the structure = PA + PB + AB + BC + CD + DA

= $$\ \frac{\ \sqrt{10}}{4}\ $$ + $$\ \frac{\ \sqrt{10}}{4}\ $$ + $$\ \frac{\ 1}{2}$$ + $$\ \frac{\ 1}{2}$$ + $$\ \frac{\ 1}{2}$$ + $$\ \frac{\ 1}{2}$$

= $$\left(2+\ \frac{\ \sqrt{10\ }}{2}\right)$$m

Length of 20 such structures =$$\left(2+\ \frac{\ \sqrt{10\ }}{2}\right)\times\ 20$$

= $$10\left(4+\sqrt{10\ }\right)m$$

$$\therefore\ $$ The required answer is C.