Sign in
Please select an account to continue using cracku.in
↓ →
_pluB7JG.png)
Three pouches (each represented by a filled circle) are kept in each of the nine slots in a 3 × 3 grid, as shown in the figure. Every pouch has a certain number of one-rupee coins. The minimum and maximum amounts of money (in rupees) among the three pouches in each of the nine slots are given in the table. For example, we know that among the three pouches kept in the second column of the first row, the minimum amount in a pouch is Rs. 6 and the maximum amount is Rs. 8.
There are nine pouches in any of the three columns, as well as in any of the three rows. It is known that the average amount of money (in rupees) kept in the nine pouches in any column or in any row is an integer. It is also known that the total amount of money kept in the three pouches in the first column of the third row is Rs. 4.
What is the number of slots for which the average amount (in rupees) of its three pouches is an integer?
Correct Answer: 2
We can make the following table from "the total amount of money kept in the three pouches in the first column of the third row is Rs. 4."
If the minimum and maximum value are 1, then the sum of the three pouches in the middle will be Rs 3.
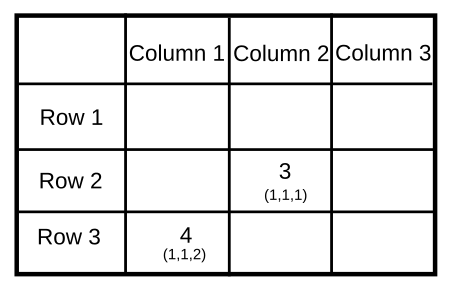
If we calculate the maximum and minimum value possible for each slot in column 1. For the slot, column 1 and row 1, the maximum value possible is 10{2,4,4} while the minimum value possible is 8{2,2,4}.
Similarly, for the slot, column 1 and row 2, the maximum value possible is 13{3,5,5} while the minimum value possible is 11{3,3,5}.
It is known that the average amount of money (in rupees) kept in the nine pouches in any column or in any row is an integer. Thus the sum of coins in a row or column must be a multiple of 9.
So, we can iterate that 10,13,4 ...{27} is the only sum possible for the slots of column 1.
We now know two elements of row 2, thus we can iterate from the maximum and the minimum value possible for the slot {cloumn 3, row 2} that 38 is the only value possible for the slot.
We can make the following table:
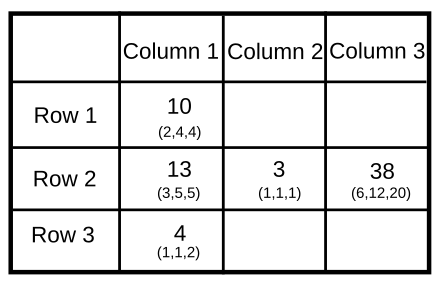
Similarly, we can find the amount for Column 2.
For the slot, column 2 and row 1, the maximum value possible is 22{6,8,8} while the minimum value possible is 20{6,6,8}.
For the slot, column 2 and row 3, the maximum value possible is 5{1,2,3} while the minimum value possible is 4{1,1,2}.
Thus {20,3,4} is the only solution possible.
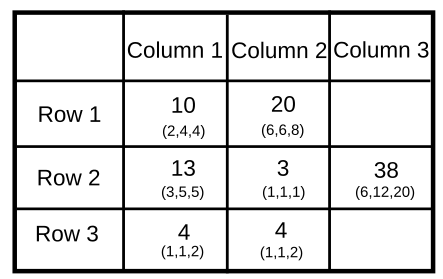
We can similarly make the following table for the last column.
.png)
Answer 2

Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
Educational materials for CAT preparation