Question 136

A chord AB of a circle $$C_1$$ of radius $$\left(\sqrt{3}+1\right)$$ cm touches a circle $$C$$ which is concentric to $$C_1$$ . If the radius of $$C$$ is $$\left(\sqrt{3}-1\right)$$ cm., the length of AB is :

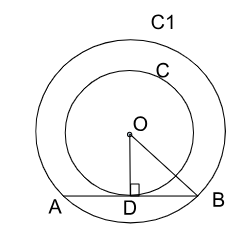
OB = $$(\sqrt{3} + 1)$$ cm

OD = $$(\sqrt{3} - 1)$$ cm

In right $$\triangle$$ ODB

=> $$(DB)^2 = (OB)^2 - (OD)^2$$

=> $$(DB)^2 = (\sqrt{3} + 1)^2 - (\sqrt{3} - 1)^2$$

=> $$(DB)^2 = (4 + 2\sqrt{3}) - (4 - 2\sqrt{3})$$

=> $$(DB)^2 = 4\sqrt{3}$$

=> $$DB = \sqrt{4\sqrt{3}}$$

=> $$DB = 2\sqrt[4]{3}$$

$$AB = 4\sqrt[4]{3}$$

View More Questions From Geometry

Create a FREE account and get: