Answer questions based on the following information:
Mulchand Textiles produces a single product of only one quality – waterproof synthetic fabric. Mr.Sharma, the cost accountant of Mulchand Textiles, estimated the costs of Mulchand Textiles for different possible monthly output levels. Before he could tabulate his estimates his computer crashed, and Mr. Sharma lost all data. Fortunately he had some printouts of some incomplete tables, charts and diagrams. The table titled “Variable Cost Estimates of Mulchand Textiles” provided the estimates of labour and material costs.

Apart from labour and material costs Mulchand Textiles incurs administrative costs of Rs. 40,000 per month, and electricity costs. Mr. Sharma recalled that estimate data of variable electricity cost had certain peculiar characteristics. Values at every 25000 sq ft of output increased in geometric progression till 150000 sq ft of output, after which values increased in arithmetic progression for every 25000 sq ft of output. Mr. Sharma remembered that the electricity cost was estimated to be Rs. 3800 for 25000 sq.ft. of output, Rs. 5700 for 50000 square feet of output and Rs. 38856.50 for 175000 square feet of output.
Solution
It is given that cost for electricity changed in geometric progression till 150000 sq ft.
Estimated electricity cost for 25000 sq. ft = Rs. 3800
Estimated electricity cost for 50000 sq. ft = Rs. 5700
Hence, we can say that common ratio of the GP that is formed by electricity cost = $$\dfrac{5700}{3800}$$ = 1.5
Therefore, estimated electricity cost for 75000 sq. ft = 5700*1.5 = Rs. 8550.
Similarly, we can calculate the electricity cost till 150000 sq. ft.
Estimated electricity cost for 200000 sq. ft = 2*Estimated electricity cost for 175000 sq. ft - Estimated electricity cost for 150000 sq. ft = 2*38856.5 - 28856.25 = Rs. 48856.75 {As these numbers are in an arithmetic sequence).
Tabulating the all data and calculating the cost per square feet.
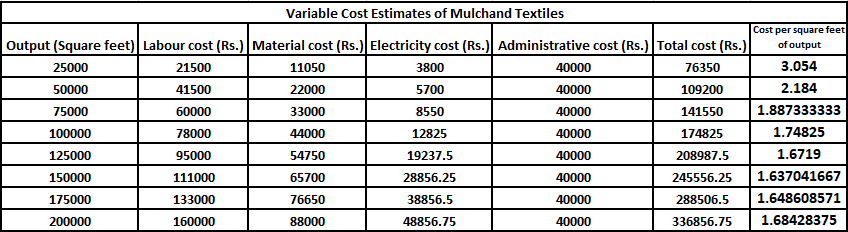
From the table, we can that cost per square feet of output is least for 150000 sq ft output. Hence, option D is the correct answer.
Create a FREE account and get:
- All Quant Formulas and shortcuts PDF
- 15 XAT previous papers with solutions PDF
- XAT Trial Classes for FREE
