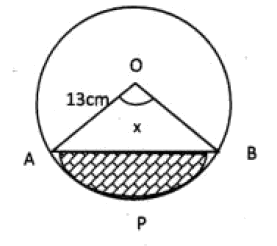
A chord AB of length 24 cm is drawn in a circle of radius 13cm. If $$\angle AOB = x^{\circ}$$, find the area of the shaded portion APB.

  

  In $$\triangle$$OAB      

          OC is drawn perpendicular to AB 

           By symmetry AC=CB=AB/2 =24/2= 12 

                                OA=13

                    $$OC^{2}=OA^{2}-AC^{2}$$

                    $$OC^{2}=13^{2}-12^{2}$$=25

                                 OC=5

So area of shaded region = Area of sector OAPB - Area of $$\triangle$$OAB

                                      =$$\frac{x}{360}*\pi*(OA)^{2}$$-$$\frac{1}{2}*(AB)*(OC)$$

                                      =$$\frac{x}{360}*\pi*(13)^{2}$$-$$\frac{1}{2}*(24)*(5)$$

                                      =$$\frac{169\pi x}{360}-60cm^{2}$$