Ram prepares solutions of alcohol in water according to customers’ needs. This morning Ram has prepared 27 litres of a 12% alcohol solution and kept it ready in a 27 litre delivery container to be shipped to the customer. Just before delivery, he finds out that the customer had asked for 27 litres of 21% alcohol solution. To prepare what the customer wants, Ram replaces a portion of 12% solution by 39% solution. How many litres of 12% solution are replaced?

Let Ram replaces $$x$$ litres of 12 % sol. with 39 % solution

Now, quality of 12 % solution in 27 litre = $$\frac{12}{100} \times 27$$

=> After replacing we have volume of 12 % solution

= $$(\frac{12}{100} \times 27) - (\frac{12 x}{100}) + (\frac{39 x}{100})$$

= $$\frac{324 + 27 x}{100}$$

This is equal to 27 litre of 21 % solution.

=> $$\frac{324 + 27 x}{100} = \frac{21}{100} \times 27$$

=> $$27x = 567 - 324 = 243$$

=> $$x = \frac{243}{27} = 9$$

Alternate Solution:

The mixture of two solutions 12% alcohol and 39% alcohol should yield 21% alcohol solution. 

Using allegation:  

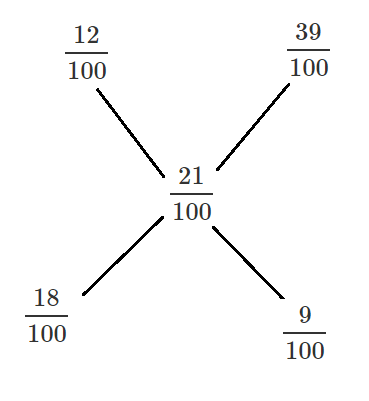
The ratio = 18/9 =2:1

So the amount of 39% solution required = 27*1/(2+1) =9