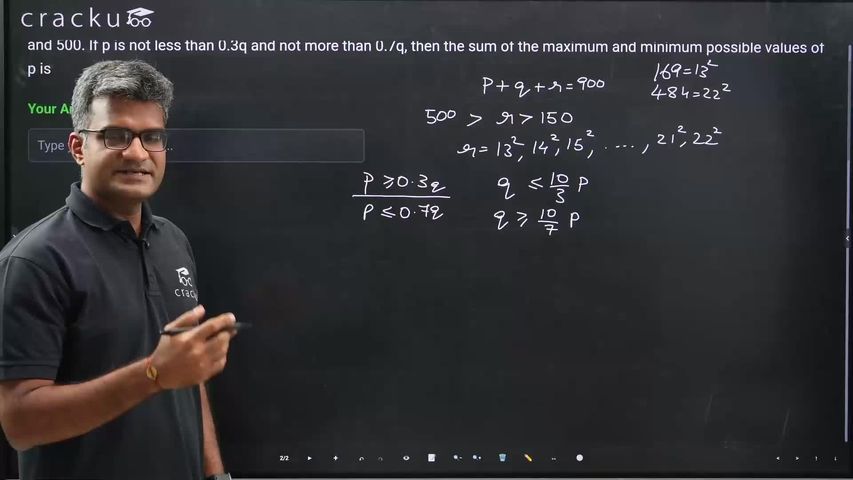
Let p, q and r be three natural numbers such that their sum is 900, and r is a perfect square whose value lies between 150 and 500. If p is not less than 0.3q and not more than 0.7q, then the sum of the maximum and minimum possible values of p is

We have $$p+q+r = 900$$, and $$r$$ is a perfect square lying between $$150$$ and $$500$$.

Let $$q$$ be a non-variable number that does not have a range.

We have $$0.3q \leq p \leq 0.7q$$,  or  $$q+0.3q \leq p+q \leq q+0.7q$$  or  $$1.3q \leq p+q \leq 1.7q$$

Also, we can rewrite $$p+q = 900-r$$

Therefore, $$1.3q \leq 900-r \leq 1.7q$$

Since the extreme values (maximum and minimum) of $$p$$ depend on the value of $$q$$ ($$0.3q$$ and $$0.7q$$), we can maximise or minimise $$r$$ to find the extreme values of $$p$$.

Since $$1.3q \leq 900-r$$, the minimum possible value of $$q$$ would be when $$1.3q = 900-r$$ and when $$r$$ is maximum. The maximum value of $$r$$ is $$484$$. We get, $$1.3q = 900-484$$, or $$q = 320$$.

This gives the minimum possible value of $$p$$ as $$0.3\times 320 = 96$$.

Since $$900-r \leq 1.7q$$. the maximum possible value of $$q$$ would be when $$900-r=1.7q$$ and when $$r$$ is minimum. The minimum value of $$r$$ is $$169$$. We get $$1.7q = 900-169$$ or $$q= 430$$

This gives the maximum possible value of $$p$$ as $$0.7\times 430 = 301$$

The sum of the maximum and minimum values of $$p$$ is $$96+301 = 397$$.