Sign in
Please select an account to continue using cracku.in
↓ →
The ratio of the number of coins in boxes A and B was 17:7. After 108 coins were shifted from box A to box B, this ratio became 37:20. The number of coins that needs to be shifted further from A to B, to make this ratio 1:1, is
Correct Answer: 272
Let the initial total number of coins in box A be $$17x$$, since the ratio of the number of coins in boxes A and B is $$17:7$$, the initial total number of coins in box B would be $$7x$$.
After $$108$$ coins are shifted from box A to box B, the number of coins in box A would be $$17x-108$$ and in box B would be $$7x+108$$. We have,
$$\dfrac{17x-108}{7x+108} = \dfrac{37}{20}$$
$$\Rightarrow 340x - 2160 = 259x + 3996$$
$$\Rightarrow 81x = 6156$$ or $$x= 76$$
Therefore, the total number of coins in the two boxes combined are $$(17+7)*76 = 1824$$, half of which is $$912$$. The number of coins in box B currently is $$7*76+108 = 640$$. The number of coins needed to make the coins equal in both the boxes is, $$912-640 = 272$$.
Thus, $$272$$ coins will be transferred from box A to box B to make the number of coins equal (1:1) in both the boxes.
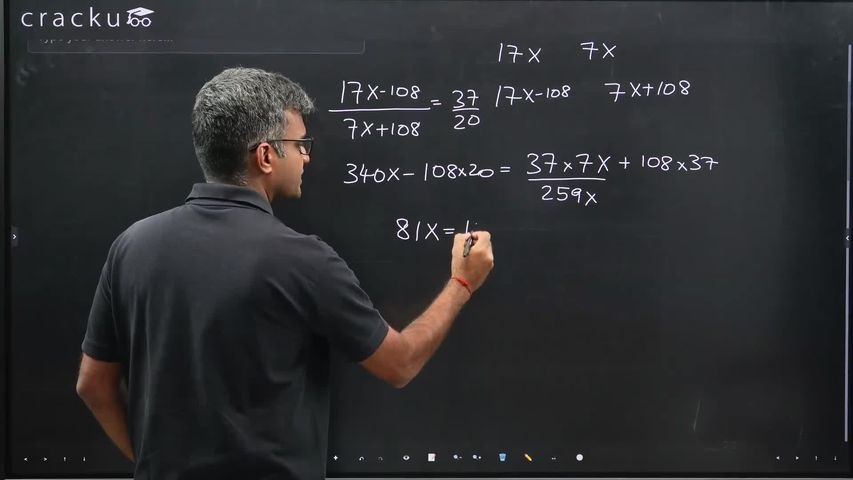
Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
Educational materials for CAT preparation