Read the following scenario and answer the THREE questions that follow.
Brijbhushan, a microfinancier, lends money at the rate of Rs.10 per square meter to small farmers at a village. He charges an annual interest rate of 10%. All the farming plots in that village are rectangular, with areas varying between a minimum of 1000 square meters and a maximum of 10,000 square meters.
This year, Brijbhushan has lent money only to five farmers: Aditya, Binod, Chhuttan, Dabloo and Govind. The perimeter of Chhuttan’s plot is 250 meters, with the length and width being at a ratio of 4:1. Aditya’s plot has an area three times the area of Govind’s plot. The area of Aditya’s plot is also the average of the areas of Govind’s plot and Dabloo’s plot. The plots belonging to Aditya, Binod and Dabloo are of the same width, but of different lengths. Moreover, the length of Binod’s plot is the sum of the lengths of Aditya’s plot and Dabloo’s plot.
What is the MAXIMUM possible value of the total loan Brijbhushan has given to these five farmers?
Solution
Let the name of farmers be A,B,C,D,G for simplicity.
Let the area of G's plot be x $$m^2$$.
Area of A's plot = 3x $$m^2$$
Let area of D's plot be y $$m^2$$.
The area of A's plot is the average of the area of D's and G's plot.
3x = $$\ \frac{\ x+y}{2}$$
y = 5x $$m^2$$
The width of the plot of A,B and D is the same and the lengths are different. Let the length of the plot of A,B and D be l1,l2 and l3 respectively and the width be y.
We got the following table.
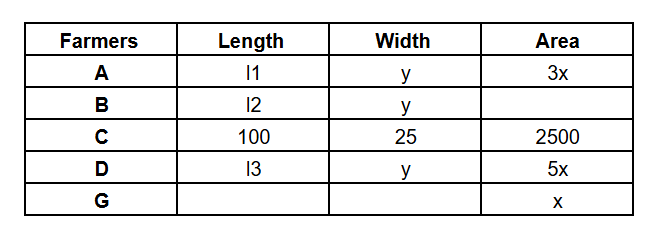
From A's plot, $$l1\times\ y=3x$$
$$l1=\ \frac{\ 3x}{y}$$
From D's plot, $$l3\times\ y=5x$$
$$l3=\ \frac{\ 5x}{y}$$
The length of B's plot is the sum of the length of A's plot and D's plot.
l2 = l1 + l3 = $$\frac{\ 8x}{y}$$
Hence, the area of B's plot = $$l2\times\ y=8x$$
The required final table is :
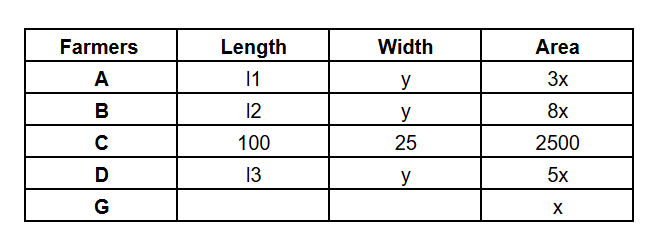
Total area of all plots = 2500 + 17x
Total loan given by Brijbhushan = $$Rs\ \left(2500+17x\right)\times\ 10$$
Since, we have to maximize the loan amount, we have to maximize the value of x.
The largest area of a land = $$10000\ m^2$$ (Given)
Among the farmers, B will have the land with the largest area.
8x = 10000 $$m^2$$
x = 1250 $$m^2$$
Hence, maximum loan given by Brijbhushan = $$Rs\ \left(\left(1250\times\ 17\right)+2500\right)\times\ 10$$ = Rs 237500
$$\therefore\ $$ The required answer is C.
Create a FREE account and get:
- All Quant Formulas and shortcuts PDF
- 15 XAT previous papers with solutions PDF
- XAT Trial Classes for FREE
