Ramesh and Reena are playing with triangle ABC. Ramesh draws a line that bisects $$\angle BAC$$; this line cuts BC at D. Reena then extends AD to a point P. In response, Ramesh joins B and P. Reena then announces that BD bisects $$\angle PBA$$, hat a surprise! Together, Ramesh and Reena find that BD= 6 cm, AC= 9 cm, DC= 5 cm, BP=8 cm, and DP = 5 cm.

How long is AP?

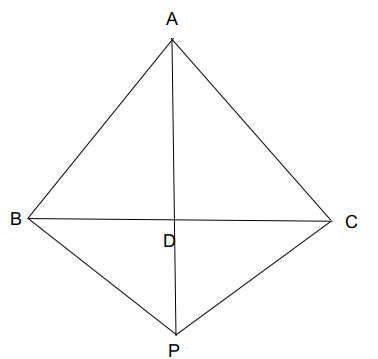
Given: 

BD= 6 cm, AC= 9 cm, DC= 5 cm, BP=8 cm, and DP = 5 cm.

Since AD is the angular bisector applying the angular bisector theorem we have :

$$\frac{AB}{BD}=\ \frac{AC}{CD}$$

Hence : Considering AB = x cm.

$$\frac{9}{5}=\ \frac{x}{6}$$

x = 10.8 cm.

Now since BD is the angular bisector for angle PBA we have :

Applyinh the internal angle bisector theorem :

$$\frac{PB}{PD}=\ \frac{BA}{AD}$$

Considering AD = y cm.

$$\frac{8}{5}\ =\ \frac{10.8}{y}$$

y = 6.75 cm.

AP = AD + DP.

= 6.75 + 5 = 11.75 cm