What is the difference between the number of tickets booked to Station C and the number of tickets booked to Station D?

Assuming the tickets from A - C, A - D, and A - E to be $$a,b$$ and $$c$$, respectively. Also, assuming the tickets from C - D and C - E to be $$x$$ and $$y$$, respectively. We are also given that the number of tickets from A - C is equal to the number of tickets booked from A - E, so the value of $$a=c$$. We are also given that 40 tickets were booked from B to C, and 30 tickets were booked from B to E. Other information provided is that no tickets were booked from A to B, from B to D, or from D to E.

Putting all the given information in the table, we get,

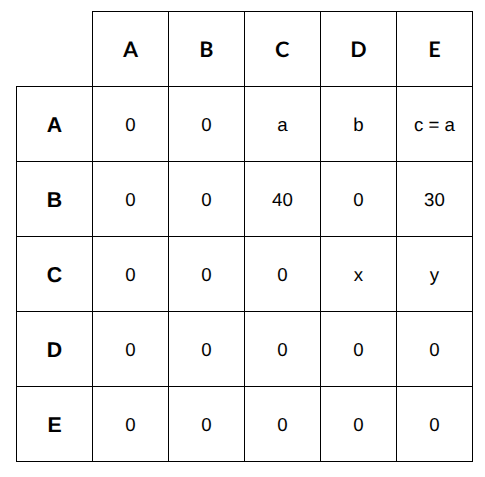
From the above table, the tickets in the segments A - B, B - C, C - D and D - E can be calculated as,

A - B $$=a+b+c=2a+b$$

B - C $$=a+b+c+30+40=2a+b+70$$

C - D $$=a+b+x+y+30$$

D - E $$=c+y+30=a+y+30$$

We are given that segment C - D had an occupancy factor of 95%. We can calculate the number of seats occupied in the segment C - D as,

Seats occupied in segment C - D $$=\dfrac{95}{100}\times\ 200\ =\ 190$$

We are given that the B - C segment had more occupancy than the C - D segment. We are also given that a, b, c, x and y are multiples of 10 as per clue 6.

We also know that the people on board in a segment cannot be more than 200. The only value greater than 190 that is a multiple of 10 is 200. So, B - C segment had 200 seats occupied.

Equating it with the above equation, we get,

$$2a+b+70=200$$

$$2a+b=130$$ --(1)

$$a+b+x+y+30 = 190$$

$$a+b+x+y=160$$ --(2)

We are also given that among the seats reserved on segment D - E, exactly four-sevenths were from stations before C. The seats reserved on segment D - E before station C are a + 30.

Equating the expressions, we get,

$$\dfrac{4}{7}\left(a\ +\ y\ +\ 30\right)\ =\ a\ +\ 30$$

$$a\ +\ y\ +\ 30\ =\ \dfrac{7}{4}\left(a\ +\ 30\right)$$ ---(3)

So, the seats occupied during D - E $$=a\ +\ y\ +\ 30\ =\ \dfrac{7}{4}\left(a\ +\ 30\right)$$

We know that this value has to be an integer.

We are given that the number of tickets booked from A to C was higher than that from B to E. This means that the value of a > 30.

We know that a and b are positive multiples of 10, so the possible values of a that are greater than 30 and satisfy the equation (1) are 40, 50 and 60.

The only value of a at which the equation (3) is an integer is when $$a+30$$ is a multiple of 4, and the only value out of the above values that satisfies the condition is when $$a=50$$, as at $$a=40$$ and 60, the value of $$a+30$$ is not a multiple of 4.

We can conclude that the value of $$a=50$$, and substituting in (1), we get the value of $$b=30$$.

Substituting in (3), we get,

$$50\ +\ y\ +\ 30\ =\ \frac{7}{4}\left(50\ +\ 30\right)$$

$$\ y\ +\ 80\ =\ 140$$

$$\ y\ =\ 60$$

Substituting all the values in (2), we get,

$$50\ +\ 30\ +\ x\ +\ 60\ =\ 160$$

$$x\ =\ 20$$

Putting all the values in the table, we get,

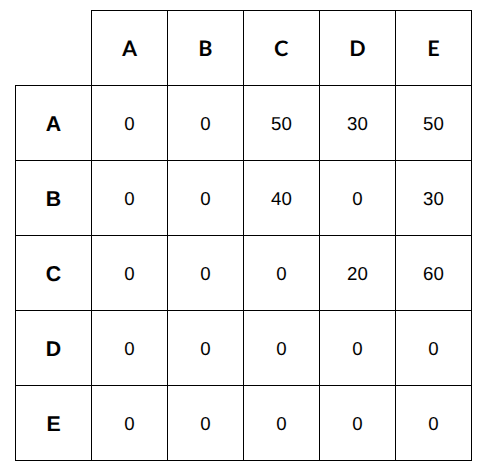
A - B $$=a+b+c=2a+b=130$$

B - C $$=a+b+c+30+40=2a+b+70=200$$

C - D $$=a+b+x+y+30=190$$

D - E $$=c+y+30=a+y+30=140$$

The number of tickets booked to station C = 50 + 40 = 90

The number of tickets booked to station D = 30 + 20 = 50

Difference = 90 - 50 = 40.

Hence, the correct answer is 40.