Sign in
Please select an account to continue using cracku.in
↓ →
There are six spherical balls, B1, B2, B3, B4, B5, and B6, and four circular hoops H1, H2, H3, and H4.
Each ball was tested on each hoop once, by attempting to pass the ball through the hoop. If the diameter of a ball is not larger than the diameter of the hoop, the ball passes through the hoop and makes a “ping”. Any ball having a diameter larger than that of the hoop gets stuck on that hoop and does not make a ping.
The following additional information is known:
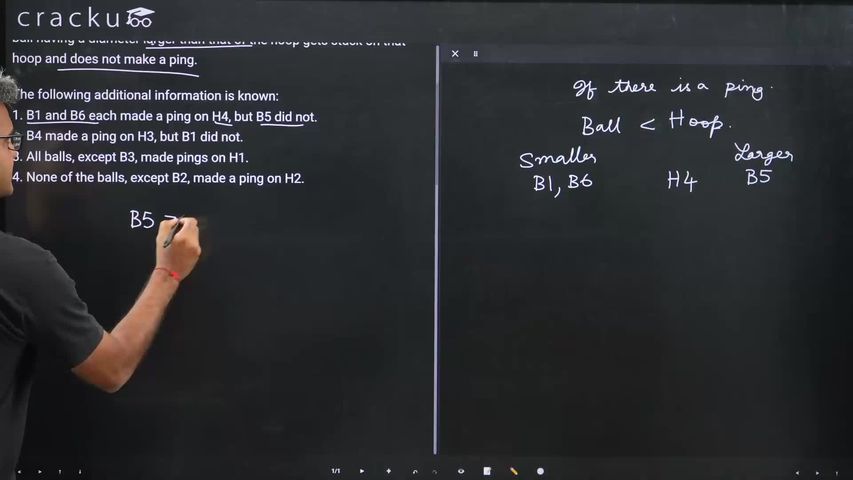
1. B1 and B6 each made a ping on H4, but B5 did not.
2. B4 made a ping on H3, but B1 did not.
3. All balls, except B3, made pings on H1.
4. None of the balls, except B2, made a ping on H2.
What BEST can be said about the total number of pings from all the tests undertaken?
Let us try to arrange the hoops and the spheres in increasing order of their diameter according to the information given,
In clue 1, we are given that B1 and B6 made a ping on H4, and B5 did not.
So, we can definitely say that,
(B1, B6) < H4 < B5 --(1)
In clue 2, we are given that B4 made a ping on H3, but B1 did not.
So, we can definitely say that,
B4 < H3 < B1 --(2)
In clue 3, we are given that all balls, except B3, made pings on H1.
So, we can definitely say that,
(B1, B2, B4, B5, B6) < H1 < B3 --(3)
In clue 4, we are given that none of the balls, except B2, made a ping on H2.
So, we can definitely say that,
B2 < H2 < (B1, B3, B4, B5, B6) --(4)
Combining (1) and (2), we can definitely say that
B4 < H3 < B1 < H4 < B5 --(5)
The only ball for which we do not have enough information is about B6, as it can be either less than H3 or greater than H3 and less than H4.
Combining (3), (4) and (5), we get,
B2 < H2 < B4 < H3 < B1 < H4 < B5 < H1 < B3
The sphere B6 can be placed in 2 positions, giving us two possible inequalities, which are
B2 < H2 < (B4, B6) < H3 < B1 < H4 < B5 < H1 < B3
B2 < H2 < B4 < H3 < (B1,B6) < H4 < B5 < H1 < B3
The position of B6 is unclear, and except for that, all the other positions are fixed.
In the first case, the number of pings possible can be calculated as 4 for B2, 3 for B4, 3 for B6, 2 for B1, 1 for B5 and 0 for B3. In total, the number of pings possible in the 1st case is 4 + 3 + 3 + 2 + 1 = 13.
In the second case, the number of pings possible can be calculated as 4 for B2, 3 for B4, 2 for B6, 2 for B1, 1 for B5 and 0 for B3. In total, the number of pings possible in the 2nd case is 4 + 3 + 2 + 2 + 1 = 12.
So, the total number of pings can be 12 or 13.
Hence, the correct answer is Option A.
Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
Educational materials for CAT preparation