Carpenter Rajesh has a circular piece of plywood of diameter 30 feet. He has cut out two disks of diameter 20 feet and 10 feet. What is the diameter of the largest disk that can be cut out from the remaining portion of the plywood piece?

It is given that the 3rd disk also has the maximum diameter. This is possible only when all 3 discs touch each other externally. 

Also the sum of the diameter of the two disks is 10+20 = 30 feets. Hence, we can say that centres of these two disk lie on a diameter of original plywood.The figure can be drawn as shown below,

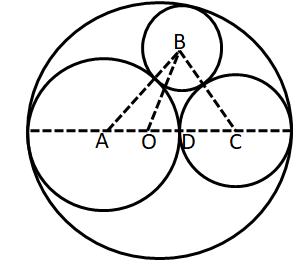
Here, in the diagram O is the centre of original disk. A and C are the centres of disks having radius 10 feet and 5 feet respectively. D is the touching point of circles with centre A and C.

Let 'x' be the radius of the disk that is to be cut out from the remaining part.

We can say that AO = OD = CD = 5 feet. Also, AB = 10+x, BC = 5+X, OB = 15-x and AC = 15 feet. 

Also, let 'y' be the length of BD.

By applying apollonius theorem in triangle ABD,

$$AB^2+BD^2=2(OB^2+OD^2)$$

$$(10+x)^2+y^2=2((15-x)^2+5^2)$$

$$x^2+20x+100+y^2=500-60x+2x^2$$

$$y^2 - x^2+80x=400$$ ... (1) 

Similarly, by applying apollonius theorem in triangle OBC,

$$OB^2 + BC^2 = 2(BD^2+DC^2)$$

$$(15-x)^2 + (5+x)^2 = 2(y^2+5^2)$$

$$2x^2-20x+250=2y^2+50$$

$$2x^2-2y^2-20x+200=0$$ ... (2) 

By equation (1) and (2) we can say that, 

$$160x-20x+200=800$$

$$x=600/140 = 30/7$$

Therefore, the diameter of the largest disk that can be cut out from the remaining portion of the plywood piece = 2*30/7 = 8.57 feet. Hence, option C is the correct answer.