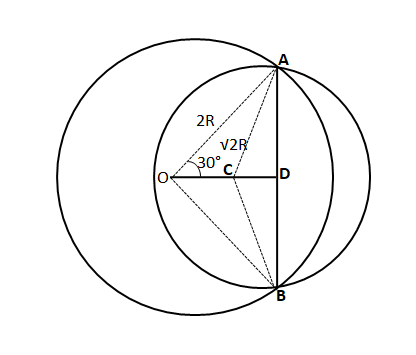
Two circles with radius 2R and $$\sqrt{2R}$$ intersect each other at points A and B. The centers of both the circles are on the same side of AB. O is the center of the bigger circle and ∠AOB is 60°. Find the area of the common region between two circles.
Solution
Let us draw the diagram according to the given info,
We can see that AD = AO*cos60° = 2R*$$\dfrac{1}{2}$$ = R
In triangle, ACD
$$\Rightarrow$$ $$sinACD=\dfrac{AC}{AC}$$
$$\Rightarrow$$ $$sinACD=\dfrac{R}{\sqrt{2}*R}$$ = $$\dfrac{1}{\sqrt{2}}$$
$$\Rightarrow$$ $$\angle$$ ACD = 45°
By symmetry we can say that $$\angle$$ BCD = 45°
Therefore we can say that $$\angle$$ ACB = 90°
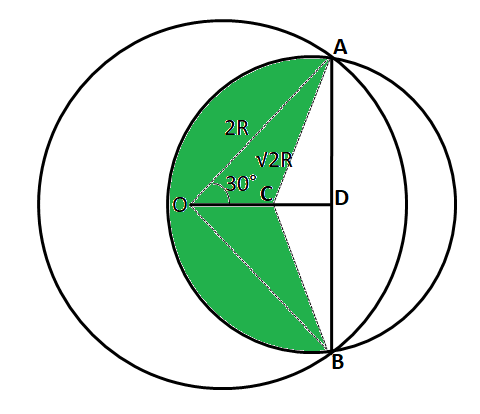
Hence, the area colored by green color = $$\dfrac{270°}{360°}*\pi*(\sqrt{2}R)^2$$ = $$\dfrac{3}{2}*\pi*R^2$$ ... (1)
Area of triangle ACB = $$\dfrac{1}{2}*R*2R$$ = $$R^2$$ ... (2)
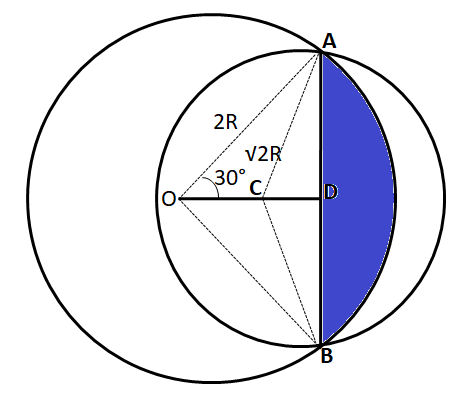
Area shown in blue color = $$\dfrac{60°}{360°}*\pi*(2R)^2-\dfrac{\sqrt{3}}{4}*(2R)^2$$ = $$\dfrac{2}{3}*\pi*R^2-\sqrt{3}*R^2$$ ... (3)
By adding (1) + (2) + (3)
Therefore, the area of the common region between two circles = $$\dfrac{3}{2}*\pi*R^2$$ + $$R^2$$ + $$\dfrac{2}{3}*\pi*R^2-\sqrt{3}*R^2$$
$$\Rightarrow$$ $$(\dfrac{13\pi}{6}+1-\sqrt{3})R^2$$
Hence, option C is the correct answer.