A ladder is placed along a wall such that its upper end is touching the top of the wall. The foot of the ladder is 10 ft away from the wall and the ladder is making an angle of $$60^{0}$$ with the ground. When a man starts climbing on it, it slips and now ladder makes an angle of 30° with ground. How much did the ladder slip from the top of the wall?

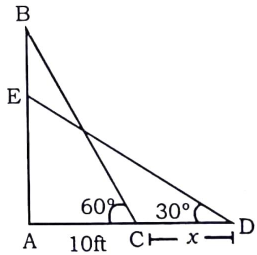
Given : BC is the initial position of the ladder, and DE is its final position. So, DE = BC (as both are the same ladders)

To find : CD = $$x=?$$

Solution : In $$\triangle$$ ABC,

=> $$cos(60^\circ)=\frac{AC}{BC}$$

=> $$\frac{1}{2}=\frac{10}{BC}$$

=> $$BC=10\times2=20$$

Thus, $$DE=BC=20$$

Similarly, in $$\triangle$$ ADE,

=> $$cos(30^\circ)=\frac{AD}{DE}$$

=> $$\frac{\sqrt3}{2}=\frac{x+10}{20}$$

=> $$x+10=10\sqrt3$$

=> $$x=10(\sqrt3-1)$$

=> $$x=10\times0.732=7.32$$

$$\therefore$$ The ladder slipped 7.32 ft

=> Ans - (C)