In a battle, the commander-in-chief arranges his soldiers in a formation of three concentric circles. The radii of the circles are in an arithmetic progression: the smallest radius is 70m (meters) and the largest is 140m.
If each soldier is to be separated from the adjacent soldiers standing on the same circle by 1m, how many soldiers are required to complete the formation? (Consider π = 22/7.)

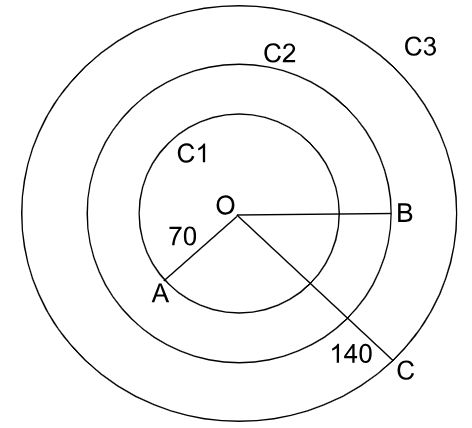
Three concentric circles C1, C2 and C3 with the radius OA, OB and OC are drawn. 

OA, OB and OC are in AP (given). 

OA = 70m, OB = (70 + d)m, OC = (70 + 2d)m , where, d is the common difference. 

OC = 70+2d = 140 (given) 

d = 35m 

OB = 70 + 35 = 105m  

The soldiers are standing on the circumference of these three circles at a distance of 1m. Hence, to find the total number of soldiers, we have the find the length of the circumference of all three circles. 

Total circumference = $$2\pi\ \left(r1+r2+r3\right)$$

= 2 $$\times\ $$ $$\ \frac{\ 22}{7}\times\ \left(70+105+140\right)$$  = 1980

Hence, the total number of soldiers are 1980.

$$\therefore\ $$ The required answer is D.