Top 100 CAT Quant Questions with Solutions PDF
Cracku's collection of Top 100 CAT Quant Questions is here to help you boost your quant solving skills. These questions cover essential Quant topics and are designed to strengthen your grasp on high-level CAT quant problems. Perfect for anyone looking to achieve a top score, these questions will get you ready for the toughest challenges on exam day.
Why Practice with Top 100 Quant Questions for CAT?
The CAT Quant section can be challenging, and practicing high-quality questions is key to success. This set of Top 100 CAT Quant Questions:
- Builds your understanding of core concepts
- Sharpens problem-solving speed and accuracy
- Prepares you for high-level CAT quant questions similar to what you’ll see in the actual exam
With this below given 100 CAT Quant Questions with Solutions PDF, you’ll find detailed solutions and step-by-step explanations for each problem, helping you tackle even the toughest topics.
Also Check, CAT Expected Questions 2024, Section-wise Questions PDF
Question 1
How many points in the region enclosed by $$x\geq0$$, $$y\leq0$$ and $$7x-9y\leq63$$ have integral coordinates?
correct answer:-1
Question 2
If A and B are natural numbers such that $$A \leq 10$$ and $$B \leq 15$$, what is the number of unique values that the expression 4A+9B will take?
correct answer:-4
Question 3
Rahul invested a total of 10,000 rupees in two banks. Bank A offers simple interest at 6% pa and Bank B offers compound interest at 8% pa. After 2 years he terminates both the deposits. He calculated his total interest as Rs. 1432. What was the amount he invested in Bank A?
correct answer:-2
Question 4
The product of 4 consecutive odd natural numbers is 156009. Find the sum of these 4 odd integers.
correct answer:-80
Question 5
Find the number of ways in which the number $$6561^2$$ can be written as a product of 3 factors.
correct answer:-4
Question 6
We are told that f(x) is a polynomial function such that f(a)f(b) = f(a) + f(b) + f(ab) - 2 and f(4) = 17, find the value of f(7).
correct answer:-50
Question 7
In a school, every student likes one of the three sports - Cricket, Football, Rugby. 65% of the students like Cricket, 86% like Football and 57% of the students like Rugby. What is the maximum percentage of students who like exactly two sports?
correct answer:-1
Question 8
Which condition will a,b,c satisfy if the set of equations 3x + 4y + z = a, 2x + 6y + 4z = b and x - y - 2z = c has atleast 1 solution ? Also a + b + c $$\neq$$ 0.
correct answer:-4
Question 9
A man can complete a job in 40 days working 6 hours a day. He started the work and on the second day, another person who can complete the job in half the time as the first person joined him. On the third day, a person who can complete the job thrice as fast as the first person joined them. This process continues till the entire work is completed. After how many days from the start will the work be completed (Every day consists of 8 hours of work)?
correct answer:-2
Question 10
The cost of 4 pens, 10 pencils and 14 erasers at a stationery shop is Rs 120. At the same shop, the cost of 6 pens and 10 erasers is Rs 60 more than 12 pencils. By how much amount (in Rs.) does the cost of 78 pencils and 2 erasers exceed the cost of 12 pens?
correct answer:-120
Question 11
A shopkeeper sells 1 kg rice to two customers Rani and Vani. For Rani he charges exactly the cost price but under weighs the quantity by 10%. For Vani he sells at 20% more than cost price but over weighs the quantity by 10%. What is his overall profit/ loss percentage?
correct answer:-2
Question 12
207 people who attend “Bold Gym” in Kondapur take four types juices Apple, Orange, Pomegranate and Mango. There are a few people who do not take any of the juices. It is known that for every person in the Gym who takes atleast ‘N’ types of juices there are 2 persons who take atleast ‘N-1’ juices for N = 2, 3 and 4. If the number of people who take all four types of juices is equal to the number of people who do not take any juice at all, what is the number of people who take exactly 2 types of juices?
correct answer:-2
Question 13
Jay has 3 types of boxes Large, medium and small. He first puts 10 large boxes on a table. He leaves some of these boxes empty and in all the other boxes puts 7 empty medium sized boxes. He then leaves some of the medium sized boxes empty and places 7 empty small boxes in the other medium sized boxes. If 82 boxes on the table were empty, then what is the total number of boxes he used? (All large boxes are of the same size, all medium boxes are of the same size and all small boxes are of the same size)
correct answer:-3
Question 14
Ramesh and his son were born on the same date and the age of Ramesh was 4 times that of his son when he was as old as his son is now. What could be the sum of present ages of Ramesh and his son on their birthdays, if Ramesh is at-least 45 years old and his son is not more than 30 years old?
correct answer:-77
Question 15
In a farm, thirty men can do a work in fifteen days.All of them started working on the first day.On every alternate day starting from the second day, some men didn’t turn up. The number of number of men who did not turn up is equal to number of the day(i.e. number of men who didn’t turn up on second day was 2 and on fourth day was 4 and so on). In how many days can they complete total work?
correct answer:-2
Question 16
How many values of (a, b) satisfy the following equations.
a + |b| = 12 and |a| + b = 9
correct answer:-1
Question 17
N is a positive integer such that (N+1) is a factor of N!. If it is known that $$1 \leq N \leq 100$$, then how many values of ‘N’ are possible?
correct answer:-4
Question 18
The distance between point P and point Q is 1600 meters. Aman starts to walk from point P towards point Q. He has a dog with him who starts from point P and runs towards point Q. As soon as the dog reaches point Q, it turns back and heads towards P. After reaching P, it again turns back and moves towards point Q. The process keeps on repeating till Aman reaches point Q. If the ratio of Aman’s speed and the dog’s speed is 1:7, then at how many distinct points does the dog meet Aman when both of them are travelling in same direction (exclude the starting point)?
correct answer:-3
Question 19
If the real root of the cubic equation $$8a^3-12a^2-6a-1=0$$ is expressed as $$\frac{\sqrt[3]{p}+\sqrt[3]{q}+1}{r}$$ where $$p,q,r$$ are natural numbers, what is the value of $$p+q+r$$
correct answer:-8
Question 20
$$x(x+1)(x+2)(x+3) = 168 $$
For the above equation the sum of all possible real roots is P. What is the absolute value of P?
correct answer:-3
Question 21
X! has 3 more trailing zeroes than (X-2)!. How many values can X take if it is known that X lies between 1000 and 2000 (both inclusive)?
correct answer:-3
Question 22
If T = $$\frac{3}{5} + \frac{6}{5^2} + \frac{11}{5^3} + \frac{18}{5^4} + \frac{27}{5^5} + \frac{38}{5^6} + … $$
What is the value of T?
correct answer:-4
Question 23
If the roots of the equation $$ax^2 + bx + c = 0$$ are of different signs, then which of the following statements is definitely false?
correct answer:-3
Question 24
A shopkeeper buys 50 earphones at Rs 100 each. After buying, he realizes that x number of earphones are not working and cannot be sold. He marks up the price of the remaining earphones to Rs. M where M is a natural number. y number of earphones are not properly packed, and hence, the shopkeeper offered a 50% discount on them. If he sells the remaining earphones at the marked price and earns a total profit of 20%, which of the following cannot be the value of x and y?
correct answer:-2
Question 25
If $$T_{n} = \dfrac{(n+7)(n+8)}{8}$$ and $$\dfrac{1}{T_{1}}$$+$$\dfrac{1}{T_{2}}$$+$$\dfrac{1}{T_{3}}$$+ ... + $$\dfrac{1}{T_{k}}$$ = $$\dfrac{1000}{1004}$$, then find the value of $$k$$?
correct answer:-2000
Question 26
The selling price of 16 pens is the same the cost price of 25 pens. If the total discount offered on 50 pens is the same as the selling price of 14 pens then find out the markup percentage.
correct answer:-100
Question 27
A milkman has 100L of milk with him. He bought this 100L for 10000 Rs. He sells 20L of it at 80Rs per liter and replaces the sold milk by water. He then again sells 20L of the mixture at 85 Rs per liter and replaces it with water. He then sells 25L of the mixture at 90 Rs per liter and replaces it water. He then finally sells 25L at 95 Rs per liter. What is his overall profit/loss in these transactions, assume water comes free of cost? (if you feel he had a loss of X Rs the put -X as the answer and if you feel he had an overall profit of X Rs then put X as the answer)
correct answer:-1525
Question 28
If a, b and c are three real roots of the equation $$x^3 - 9x^2 - 10x + 168 = 0$$ and (a+b), (b+c) and (c+a) are the roots of the equation $$x^3+px^2+qx+r = 0$$, then what is the value of |r - p|?
correct answer:-60
Question 29
The number of integer values of 'a' for which both the roots of the equation $$ax^2+(a-4)x+a+1=0$$ are greater than 0 is
correct answer:-1
Question 30
If $$\log_{3}({\log_{81}{x})}=\log_{81}({\log_{3}{x})}$$ then find the value of $$x$$
correct answer:-2
Question 31
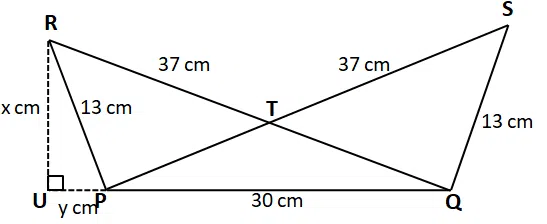
Two points R and S lie on the same side of PQ in such a way that PQ = 30 cm, PR = QS = 13 cm and PS = QR = 37 cm. If PS and QR intersect at a point T, then find out the area of $$\triangle$$ PQT(in cm$$^2$$).
correct answer:-2
Question 32
Find the product of all the values of $$3^x+2$$ such that the values of $$x$$ satisfy the following equation: $$log_3(18-3^x)=3-x$$.
correct answer:-3
Question 33
3 persons Akram, Bikram, Chandan take part in a race. Akram can give Bikram a head start of 64 feet. The head start that Chandan can give Bikram is 40 feet longer than the head start that he can give to Akram. If it is known that one person is twice as fast as one of the other two persons and the length of the track (in feet) is an integer, what is the length of the track (in feet)?
correct answer:-4
Question 34
If p+q+r =5 and pq+qr+pr = 3 where p,q,r are positive real numbers .Find the largest value which p can take
correct answer:-2
Question 35
An investor is faced with a dilemma about where to invest his savings of 10 lakhs. Scheme A gives 10% interest compounded annually for 2 years and simple interest of 20% for the next 3 years. If the amount has increased less than 60%, additional 10% is also added to it. Scheme B gives a simple interest of 10% for 2 years and compound interest of 20% for 3 years compounded annually. If the amount has increased less than 50%, additional 15% is added to it. If the investor goes with the right choice, how much does he earn over his initial investment ?
correct answer:-1073600
Question 36
Three men can build a wall in 5 days. The total money of the job is 150000. If the efficiency of the three people is in the ratio 4:5:6, what is the difference in amount received by the person receiving the most and the person receiving the least amount of money?
correct answer:-2
Question 37
A car moving towards P from Q. It develops a fault after 2 hours of journey. Due to this fault, the speed of the vehicle reduces by 20%. This results in a delay of 2 hours. After how many hours should the fault have developed to reduce the delay to 1 hour ?
correct answer:-3
Question 38
An infinite geometric progression has the sum 10. Sum of all the possible integral values of the first term is
correct answer:-180
Question 39
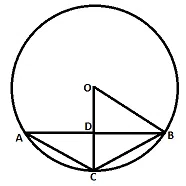
In given circle, O is the center, OB and OC are the radii. It is given that OD:DC = 2:3, angle BDC= $$105^{\tiny 0}$$ and AC=11.52 cm. If the radius of the circle is equal to 10 cm, find the area of the triangle BOC (Take sin75=0.96).
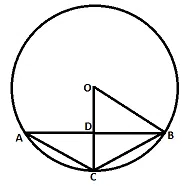
correct answer:-1
Question 40
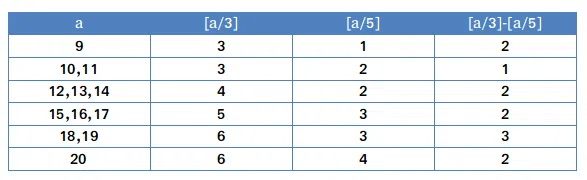
If [X] represents the greatest integer function, a is a positive integer where [a/3]-[a/5]=2 then what is the number of possible values a can take?
correct answer:-1
Question 41
PQRXYZ is a hexagon in which all its interior angles are equal. If the lengths of PQ= 1cm, QR = 4cm, RX =2cm, XY = 2cm .Then lengths of PZ and ZY are
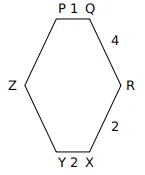
correct answer:-1
Question 42
A line passing through the point (3,0) divided the rectangle formed by lines |y-4|=2 and |x-6|=3 into two congruent parts. If the slope of the line is a/b and a,b are co-primes, the value of a+b is equal to
correct answer:-4
Question 43
If ‘$$\alpha$$’ is the root of the equation $$x^2+6x+10$$=0. Then the value of $$(\alpha+1)(\alpha+2)(\alpha+4)(\alpha+5)$$ is
correct answer:-10
Question 44
In how many ways can Nihal select 3 apples from a row of 33 apples such that there should be at least 3 apples between any selected apples. Assume that all the apples are distinct.
correct answer:-2
Question 45
What is the number of perfect cubes that can be represented as a 4-digit number in base 5?
correct answer:-4
Question 46
The number of ways in which 33 identical pens can be distributed among three boys such that each of them receives an odd number of pens is
correct answer:-1
Question 47
If $$\mid\log_{(6x+4)}{(3x-2)}\mid$$=1. What is the number of possible values of x?
correct answer:-1
Question 48
When dropped from a height 'h', balls of Type 1 bounce to height 2h/3 while balls of Type 2 bounce to height h/2. Two balls, one of Type 1 and one of Type 2, are dropped from 12m and 36m respectively. Then what is the sum of the total distance (in metres) they will travel after bouncing indefinitely?
correct answer:-168
Question 49
A semicircle is inscribed in a quarter circle as shown in the figure with radii OA and OB equal to 2$$\sqrt{21}$$ cm. What is the area of shaded region? (Take $$\pi$$=$$\frac{22}{7}$$)
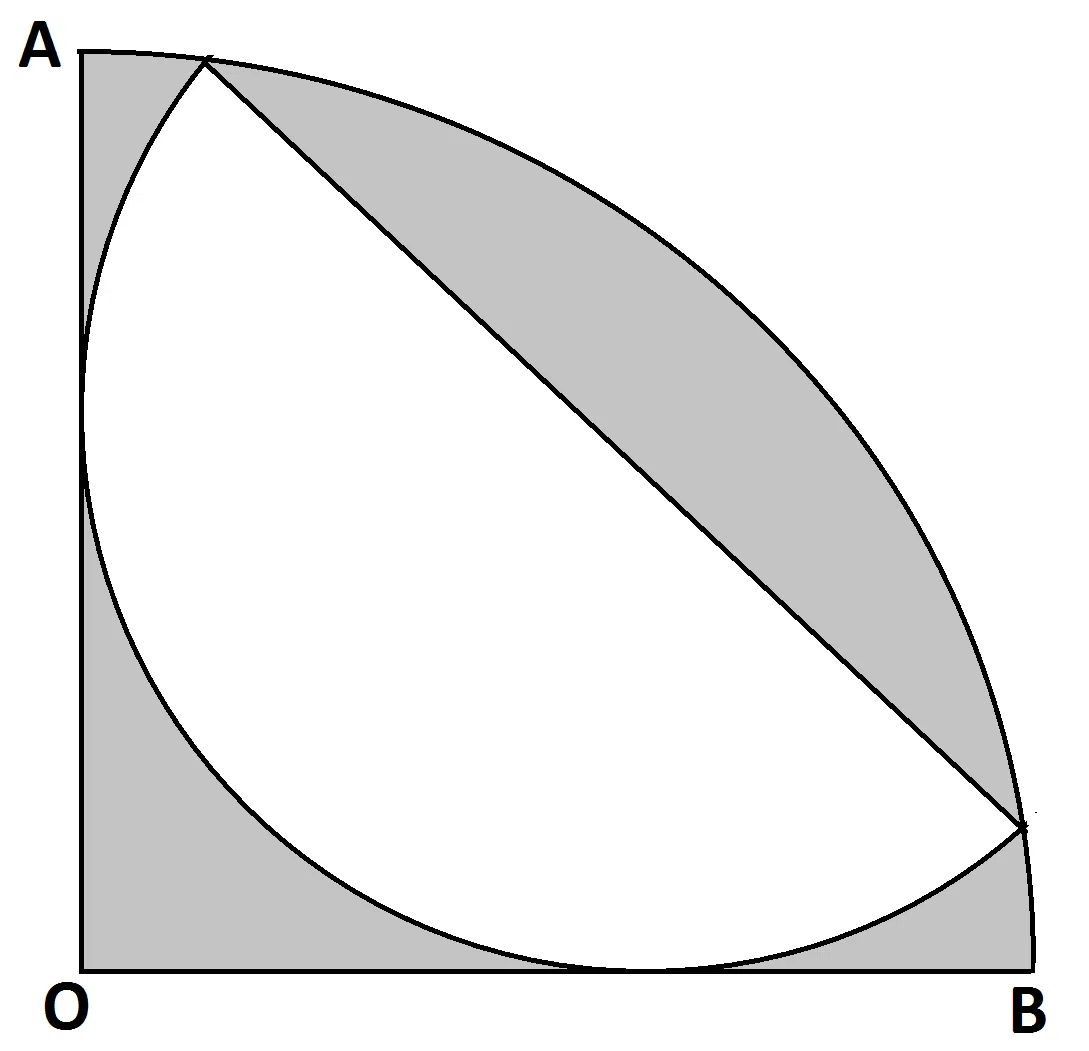
correct answer:-3
Question 50
In a company, the ratio of male and female employees is 2:3. Each employee earns either 30000 or 60000 per month. The ratio of the average male salary to the female salary is 15:16. The ratio of the number of males who make Rs 60000 to that of females who make Rs 30000 is 1:4. Find the average salary of all the employees.
correct answer:-2
Question 51
Haritha, Anita and Vasanta have red, blue and green coloured dice respectively. All three of them rolled their dice simultaneously. Then the probability that the sum of the numbers turned up on the blue and green dice is equal to the number on the red dice is
correct answer:-1
Question 52
If f(x) = $$x^2+7x+10$$, then the number of real roots of f(f(f(x))) = 0 is
correct answer:-1
Question 53
A vessel contains P litres of a mixture of water and alcohol. The ratio of the alcohol-water mixture is reversed when 10 litres water is added to it. Now 10 litres of this mixture is replaced with pure alcohol and the ratio of alcohol and water becomes 3:2. Find the value of P.
correct answer:-20
Question 54
Ram has been given the value of the first term as 6 and the common difference as 2 of an arithmetic progression. He is asked to write the sum of the first 20 terms of the series. After writing first x terms, he takes the common difference as 12 by mistake. As a result, the sum of all the terms increases by 56%, find the value of x
correct answer:-13
Question 55
A loan amount of Rs. 7200 was repaid in two equal half yearly installments. If the rate of compound interest is 50% p.a compounded semi annually, what is the amount paid in each installment?
correct answer:-5000
Question 56
Three vessels P, Q and R contain a solution of water and alcohol. The ratio of water and alcohol in vessel P and vessel Q are 2:3 and 1:4. After combining Q and R in the ratio 1:2, the resulting mixture contains the water and alcohol in the ratio 4:11. Find the percentage of water in a mixture which has P, Q and R combined in a ratio 3:5:2.
correct answer:-28
Question 57
The cost price of 6 apples is equal to the marked price of 5 mangoes. The cost price of 5 mangoes is equal to the marked price of 2 apples. If the shopkeeper gives 2 mangoes free on the selling of 6 apples and makes a profit of 87.5%, find the profit percentage on selling 1 mango at its marked price.
correct answer:-4
Question 58
In a company XYZ, there are three departments, P, Q and R. The number of employees in department P is half of the number of employees in department R. The total number of employees of Q and R is 280. If 20 employees of the department R are transferred to the department Q, then the ratio of the number of employees in department P to that of Q will be the same as the ratio of the number of employees in department Q to that of department R. Find the number of employees in department R.
correct answer:-180
Question 59
In an equilateral triangle ABC, a point P is marked on AB. The side AC is extended to Q such that APQ is a right triangle with P = 90$$^{\circ\ }$$. The area of ABC is equal to the area of APQ. If BP = 6-$$3\sqrt{2}$$, then find the value of AB?
correct answer:-4
Question 60
The graph of y = $$x^2 - 8x + 13$$ is symmetric wrt to the line x = c, then the value of c is
correct answer:-4
Question 61
Two runners are running to and fro from points A and B respectively. Theirs speeds are in the ratio 7:3. If the distance between the first and second points of intersection is 45meter, what is the distance between point A and B?
correct answer:-3
Question 62
The sum of all two-digit numbers that give a remainder of A when they are divided by 7 is 654. What is the value of A?
correct answer:-2
Question 63
In the given figure, ABCDE is a regular pentagon. If AB=AF and $$\angle$$ DCF = 90$$^{\circ\ }$$, then find the value of $$\angle$$ FAE?

correct answer:-4
Question 64
If the number of factors of N is 8 and that of 5N is 16, then the number of factors of 2*N can be
correct answer:-2
Question 65
f(x) is a polynomial function of degree 4 such that f(0) = 1, f(1)=3 , f(2) = 9 and f(3) = 19.
What will be f(-1) if the coefficient of $$x^4$$ is 2 in f(x)
correct answer:-3
Question 66
A square, ABCD has a side of length 12 cm each. An equilateral triangle, MAB exists such that M is outside the square ABCD. If a circle is drawn in such a way that it passes through the points M, C and D, then what will be the radius of that circle?
correct answer:-3
Question 67
A rectangle ABCD has sides AD = 9 and AB=12. Points E, F, and G lie on diagonal AC such that 3 AE =2AG = AC. AE = CF What is the area of the triangle BGF
correct answer:-2
Question 68
The number of even factors of S, where S= $$1^3+2^3+3^3+...\ 1000^3$$ is
correct answer:-756
Question 69
A pizza store sold pizzas in 3 sizes- Small, medium and large with diameters of pizza equal to 8 inches, 11 inches and 14 inches. If the cost of the pizza depends on the volume of the pizza and the prices of the pizza are in the ratio 2:3:4, then the ratio of thickness of the small, medium and large pizza is in the ratio-
correct answer:-1
Question 70
A water tank has 3 taps attached to it. Tap 1 fills the entire tank alone in 8 hours and is at the bottom of the tank. Tap 2 alone empties the tank in 12 hours, but it is located at the middle of the tank and tap 3, which fills the entire tank alone in 4 hours is located at a distance of 25% of the height from the top. In how many hours will the tank be filled if all the three taps are open from the beginning?
correct answer:-2
Question 71
In how many ways can we select a square of side length at most 4 units from a chess board if one square of the chess board is considered to have a side length of 1 unit?
correct answer:-174
Question 72
The values for which |(x-2)-|x+2||-5$$\ge\ $$0 holds are:
correct answer:-3
Question 73
A company was purchasing 30 barrels of oil every month during lockdown from March 2020 till August 2020. The price per barrel paid by the company increased every month by a constant amount of $10. They purchased the barrels at $25 in March 2020. In September 2020, the company then sold half of the barrels at $45 each, half of the remaining at $50 each and all the remaining barrels at $70 each. What is the company's profit in percentage?
correct answer:-4
Question 74
A function f(x) is defined as follows for $$x\in\ \left(-\infty\ ,\infty\ \right)$$
f(x) = max{$$x^2+2x+1$$,$$\left|x\right|+1$$}
Find the minimum value of f(x).
correct answer:-2
Question 75
How many ordered pairs (x,y) exist that satisfy the following inequality?
xy + 5x + 6y < 20
It has been given that x is a whole number and y is a natural number.
correct answer:-6
Question 76
Prasoon purchased a new bike M15, which soon met with an accident. He went to the service centre and the service centre charged him for repairs. The labour cost, tyre replacement cost, accessory replacement cost and the servicing costs were 5%, 15%, 25% and 35% of the total servicing cost respectively. The remaining charges were for oil replacement (brake oil, engine oil, etc.). Luckily Prasoon was the lucky customer that day and got discounts of 10% each for labour, servicing and oil replacement costs and discounts of 20% on the accessory replacement. The insurance company paid him 80% of the cost paid by him in the service centre by giving him Rs. 56,960. What was the original bill amount (before discount) for accessory replacements in Rupees?
correct answer:-20000
Question 77
A compound 'M' is to be created, one unit of which consists of 3 units of 'X', 4 units of 'Y' and 6 units of 'Z'. 1 unit of X is made by A and B in the ratio 5:7 respectively, 1 unit of Y is made by B and C in the ratio 2:3 respectively, and 1 unit of Z is made by A and D in the ratio 1:4 respectively. What is the approximate percentage contribution of A in 1 unit of M?
correct answer:-1
Question 78
Raghav went to an orphanage of 5 kids with 22 similar notebooks to gift the children. Kids in the orphanage demanded at least 1, at least 2, at least 3, at least 4 and at least 5 notebooks with no two kids demanding the same minimum number of books. In how many ways can Raghav distribute the notebooks to them?
correct answer:-330
Question 79
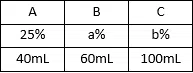
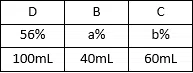
Mr Cooper has 3 alcohol solutions, A, B and C. A has 25% alcohol concentration, B has a% alcohol concentration and C has b% alcohol concentration. He mixes 40mL of A, 60mL of B and 100 mL of C to get a new solution D with a concentration of 56%. Now, he mixes 100mL of D, 40mL of B and 60mL of C to get a solution with 59.5% concentration. Find the difference between a and b.
correct answer:-1
Question 80
What is the value of x for which $$2^{\left(1+3+5+...x\right)}=\left(0.0625\right)^{-25}$$
correct answer:-3
Question 81
A telecom company has decided to come up with new sim cards. It got the permission that it could assign its customers ten-digit numbers with the constraint that the numbers should start with 7809 and the remaining 6 digits can be selected from all 10 digits, without repetition such that they appear in the sim card number in ascending order. Find the maximum number of sim card numbers the company can come up with.
correct answer:-1
Question 82
In a test, there are 34 multiple-choice questions. A correct answer fetches +3, and a wrong answer fetches -1. There is no penalty for unattempted questions. In how many ways can a student achieve 67 marks in this test?
correct answer:-3
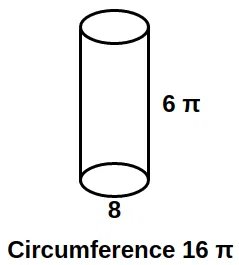
Question 83
There is a right circular cylinder which has a base diameter of 16 units and a height of $$6 \pi $$ units. An ant is at the circumference of the base of the cylinder and wants to reach the sugar cube which is placed at top-most point of diametrically opposite end from the ant. What is the minimum possible distance that ant has to travel?
correct answer:-2
Question 84
A quadratic equation f(x) = 0 exists such that f(x) = $$3x^2+9x+3$$. A second quadratic expression g(x) is formed by shifting f(x) towards the right along the x-axis by 5 units. What is the sum of the roots of equation g(x) = 0?
correct answer:-1
Question 85
If $$\log_{125}40=\ a$$ and $$\log_598=\ b$$. Then how can $$\log_{14}5$$ be represented in terms of a and b?
correct answer:-3
Question 86
It is given that $$x$$ and $$y$$ are integers such that $$ |x+3| < 7 $$ and $$ |y-4| < 8$$. What is the difference of maximum and minimum value of $$x + xy+ y $$ ?
correct answer:-144
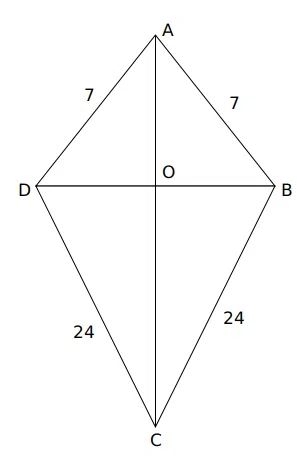
Question 87
A kite is a quadrilateral whose four sides can be grouped into two pairs of equal-length sides that are adjacent to each other. A kite is formed with length of uncommon sides as 7 and 24. If length of one of its diagonal is 25 what is the length of other diagonal?
correct answer:-1
Question 88
If $$S_n=2n^3+n^2+3n+1$$, where $$S_n$$ denotes sum to first n terms of a series. It is given that $$t_x$$, which is the xth term of the series is equal to 84, then x=?
correct answer:-3
Question 89
Find the sum of the following series up to 50 terms:
3, 1, -2, -6, -11, -17,....
correct answer:-2
Question 90
A milkman has 2 varieties of milk-water solution, solution A has 65% pure milk and solution B has 78% pure milk. He is mixing x mL of solution A with y mL of solution B such that the resultant solution has no less than 70% pure milk and no more than 72% pure milk. If y can take any value between 625mL and 630mL, both inclusive, what is the difference between the minimum and maximum value x can take? It is given that x and y are both integers.
correct answer:-1
Question 91
A survey was conducted in a society to get an estimate of how many people read the following newspapers, The Telegraph, The Economic Times and The Times of India. It was found out that 20% of people of the society read The Telegraph, 30% of people of the society read The Economic Times and 40% of the people of the society read The Times of India. If the society had a total of 600 people, what can be the maximum number of people in the society who read none of the newspapers?
correct answer:-360
Question 92
A right-angled triangle ABC has an inradius and circumradius of 4 cm and 10 cm respectively. What is the area of triangle ABC in sq. cm?
correct answer:-96
Question 93
A rectangle ABCD exists such that AB = 6 units and BC = 12 units. E and F trisect the diagonal AC in 3 equal parts. G is centroid of the triangle formed by DEF. What is the area of DGBC?
correct answer:-2
Question 94
How many 4-digit numbers exist which is divisible by 3 or 8?
correct answer:-4
Question 95
Among all the possible permutation of the word " VENKATESHAN" What is the probability that a word is chosen such that both the "A"s are before both the "E"s?
correct answer:-4
Question 96
A, B and C are 3 friends who have to go to another city Z. A has a bike that has an average speed of 40 km/hr. B and C both can walk with an average speed of 5km/hr. To minimise the time taken for them to reach the other city it was decided that C will start walking towards the city Z while A will gives a lift to B for a certain distance after which A will drop-off B and B will start walking towards Z. A will go back to pick up C and then will start moving towards city Z. They all reach the destination at the same time. What percentage of the overall journey time, did B spend walking?
correct answer:-4
Question 97
A number N is given by = $$2^5\times\ 3^8\times\ 4^2\times\ 5^3\times\ 6\times\ 7^2$$
If a certain factor of N is not divisible by 9, the probability that the factor is an odd number is $$m/n$$ where 'n' is a natural number less than 20. Find the value of m+n.
correct answer:-12
Question 98
For how many integer values of x is the inequality given by $$\log_{\left(x+1\right)}\left(x-4\right)\left(x-3\right)\ <1$$ defined?
correct answer:-3
Question 99
Ram bought pens from a wholesaler at Rs. 200 per pen. For every additional pen sold by Ram after the first one, the selling price of the pen becomes Rs.5 less than the selling price of the previous pen. Using this strategy, Ram makes a 145% profit by selling 5 pens. What is the maximum number of pens a customer can buy in a single transaction such that Ram makes a profit on every pen sold?
correct answer:-60
Question 100
For how many real non-zero integral values of x does the following inequality hold?
$$\left|x+5\left|x-32\right|+\left|24-x\right|\right|<5$$
correct answer:-3


.webp)














![Top CAT Quant Linear Equations Questions [Download PDF] Top CAT Quant Linear Equations Questions [Download PDF]](/media/cache/cb/00/cb00fafca1806baf52b208410d968299.webp)







