A quadrilateral ABCD has side AD parallel to BC. If it is given that ∠ABC = 90°, BC = 5 cm and AD = 14 cm. It is also given that the perimeter of this quadrilateral is 46 cm, then its area, in sq. cm, is

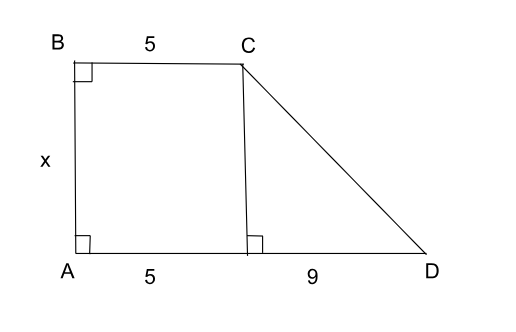
Let the value of AB be x.

Using the Pythagoras theorem, we get,

$$CD^2\ =\ x^2\ +\ 9^2$$

$$CD\ =\ \sqrt{x^2\ +\ 9^2\ }$$

The perimeter is given as,

x + 5 + $$\sqrt{x^2\ +\ 9^2\ }$$ + 14 = 46

$$\sqrt{x^2\ +\ 9^2\ }\ =\ 46\ -\ 19\ -\ x$$

$$\sqrt{x^2\ +\ 81\ }\ =\ 27\ -\ x$$

Squaring on both sides, we get,

$$x^2\ +\ 81\ \ =\ 729\ +\ x^2\ -\ 54x$$

$$54x=\ 729\ -\ 81\ =\ 648$$

$$x\ =\ 12$$ cm

$$CD\ =\ \sqrt{\ 144\ +\ 81}\ =\ 15$$ cm

Area of the quadrilateral = area if rectangle  +  area of triangle

area of rectangle = 12 * 5 = 60 sq. cm

area if triangle  =  $$\dfrac{1}{2}\ \times\ 9\ \times\ 12$$  = 54 sq. cm

Area of quadrilateral = 60 + 54 = 114 sq. cm

The correct answer is option B.