Two circles of equal radius 12cm, C1 and C2, are in such a way that they are not intersecting each other. A tangent is drawn to C1 from the intersection point of the line joining the centres of both circles, and circle C2. If the length of the tangent is given as 16cm, then what is the distance between the centres of the circles?
Solution
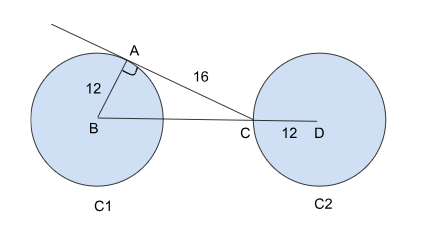
As shown in the figure above, we must calculate the length of BD. We are given the length of AC as 16 and AB as 12. The length BC can be calculated as,
$$AC^2\ +\ AB^2\ =\ BC^2$$
$$BC\ =\ \sqrt{\ AC^2\ +\ AB^2}$$
$$BC\ =\ \sqrt{\ 12^2\ +\ 16^{\ 2}}\ =\ \sqrt{\ 144+256}\ =\ 20$$
The length BD = BC + CD = 20 + 12 = 32 cm
The correct answer is option D.
Video Solution
Click on the Email ☝️ to Watch the Video Solution
