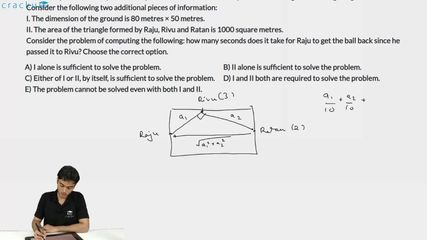
A group of boys is practising football in a rectangular ground. Raju and Ratan are standing at the two opposite mid-points of the two shorter sides. Raju has the ball, who passes it to Rivu, who is standing somewhere on one of the longer sides. Rivu holds the ball for 3 seconds and passes it to Ratan. Ratan holds the ball for 2 seconds and passes it back to Raju. The path of the ball from Raju to Rivu makes a right angle with the path of the ball from Rivu to Ratan. The speed of the ball, whenever passed, is always 10 metre per second, and the ball always moves on straight lines along the ground.
Consider the following two additional pieces of information:
I. The dimension of the ground is 80 metres × 50 metres.
II. The area of the triangle formed by Raju, Rivu and Ratan is 1000 square metres.
Consider the problem of computing the following: how many seconds does it take for Raju to get the ball back since he passed it to Rivu? Choose the correct option.

The question states that the path forms a right-angle triangle at Rivu. So, let's consider the distance from Raju to Rivu as x and that from Rivu to Ratan as y.

i)

Now, $$\triangle\ ABC$$ form a right-angled triangle. Using Pythagoras theorem

$$AB^2+BC^2=AC^2$$

=>$$x^2+y^2=80^2=6400$$ --->1

The area of $$\triangle\ ABC$$ is $$\frac{1}{2}\cdot b\cdot h$$=$$\frac{1}{2}\cdot x\cdot y$$ ---->2

If we consider the base of the triangle as AC of length 80(side of rectangle) and height as altitude from B of length 25 (half the breadth of rectangle), we can get the area as $$\frac{1}{2}\cdot b\cdot h$$=$$\frac{1}{2}\cdot 80\cdot 25=1000$$.

Now, use this in equation 2.

$$\frac{1}{2}\cdot x\cdot y$$=1000

xy=2000--->3

$$\left(x+y\right)^2=x^2+y^2+2xy$$=6400+4000=10400

x+y=20$$\sqrt{\ 26}$$

This is the distance the ball travels at 10m/s. The time taken is 2$$\sqrt{\ 26}$$+5 sec for holding.

So, 1 alone is sufficient.

ii) Given the area of the triangle is 1000

$$\frac{1}{2}\cdot x\cdot y$$=1000

=> xy=2000

With this alone, we can't find the travel time.