Please enter the following details
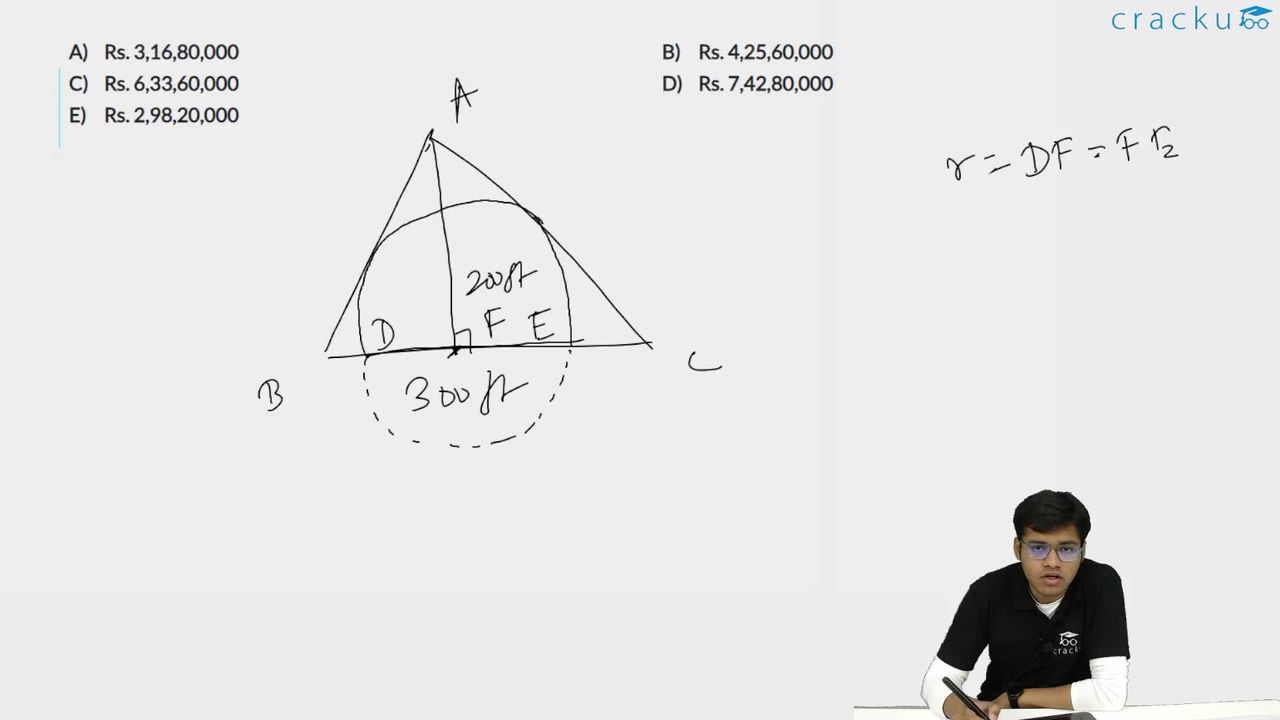
A farmer has a triangular plot of land. One side of the plot, henceforth called the base, is 300 feet long and the other two sides are equal. The perpendicular distance, from the corner of the plot, where the two equal sides meet, to the base, is 200 feet. To counter the adverse effect of climate change, the farmer wants to dig a circular pond. He plans that half of the circular area will be inside the triangular plot and the other half will be outside, which he will purchase at the market rate from his neighbour. The diameter of the circular plot is entirely contained in the base and the circumference of the pond touches the two equal sides of the triangle from inside.
If the market rate per square feet of land is Rs. 1400, how much does the farmer must pay to buy the land from his neighbour for the pond? (Choose the closest option.)
.png)
The line AC is tangent to the circle. So, the line DE is perpendicular to AC and is radius to the circle.
Look at the $$\triangle\ $$ADC and $$\triangle\ $$DEC. $$\angle\ $$DAC = $$\angle\ $$EDC, $$\angle\ $$C=$$\angle\ $$C. And both D and E are right angle triangles.
So, both the triangles are similar.
$$\triangle\ $$ ADC is a right-angled triangle.
$$AC^2$$=$$AD^2$$+$$DC^2$$
$$AC^2$$=$$200^2+150^2=250^2$$
AC=250, AD=200, DE=r, DC=150
$$\frac{AD}{DE}=\frac{AC}{DC}$$
$$\frac{200}{r}=\frac{250}{150}$$
$$\Rightarrow$$ r=120.
Given half pond is inside the triangle, so he has to only buy half the area of the circle.
Cost for buying area of semi circle =$$\pi\ \frac{r^2}{2}$$*1400=$$\pi\ \frac{120^2}{2}$$*1400= 3,16,80,000
Create a FREE account and get:
- All Quant Formulas and shortcuts PDF
- 15 XAT previous papers with solutions PDF
- XAT Trial Classes for FREE
