In $$\triangle ABC$$, $$AB =AC= 12$$ cm and $$D$$ is a point on side $$BC$$ such that $$AD= 8$$ cm. If $$AD$$ is extended to a point $$E$$ such that $$\angle ACB = \angle AEB$$, then the length, in cm, of $$AE$$ is

Based on the information provided, we can construct the following diagram;

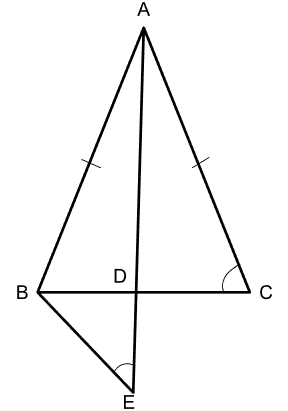
We have $$AB = AC = 12$$ cm, and $$AD = 8$$ cm. And $$\angle ACB = \angle AEB$$

Since the triangle is isosceles, $$\angle ACB = \angle AEB = \angle ABC$$ (or $$\angle ABD$$)

In $$\triangle ABE$$ and $$\triangle ADB$$,

$$\angle BAE =\angle DAB$$ and $$\angle AEB = \angle ABD$$. Therefore, by AA similarity criterion, $$\triangle ABE \sim \triangle ADB$$

Hence, we get,

$$\dfrac{AB}{AD}=\dfrac{AE}{AB}$$  or  $$\dfrac{12}{8} = \dfrac{AE}{12}$$  or  $$AE=18$$ cm.