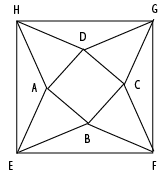
In the picture below, EFGH, ABCD are squares, and ABE, BCF, CDG, DAH are equilateral triangles. What is the ratio of the area of the square EFGH to that of ABCD?

Let the sides of the smaller square be $$x$$ units and the sides of the larger square be $$y$$ units.

Construct diagonal HF on the larger square. Let the point of intersection of AD and diagonal be I and point of intersection of BC and diagonal be J.  

We know that since EFGH is a square, the diagonal will bisect the angle. Therefore $$\angle EHF=45^{o}$$

Observe $$\triangle AEH$$ and $$\triangle DHG$$ : 

AE=AH=DH=DG = $$x$$ units and EH=HG=$$y$$ units. 

Thus by SSS property, $$\triangle AEH \cong \triangle DHG$$

Thus, we know that $$\angle$$AHE=$$\angle$$DHG

Also, $$\angle$$AHE+$$\angle$$DHG+$$\angle$$AHD= $$90^{o}$$ (angle of a square)

$$ \Rightarrow (2 \times \angle AHE)+ 60^{o} = 90^{o}$$ (angle of an equilateral triangle)

$$ \Rightarrow (2 \times \angle AHE) = 30^{o}$$

$$ \Rightarrow \angle AHE = 15^{o}$$

Since $$\angle AHE = 15^{o}, \angle AHI = 45^{o}-15^{o} = 30^{o} $$

Since $$30^{o}= \dfrac{60^{o}}{2}$$ we can say that HF is the angle bisector of $$\angle$$AHD 

Since $$\triangle$$AHD is an equilateral triangle, we know that the angle bisector, median and altitude will all be the same line ie HI in this case. 

By symmetry, we know that JF will also be the angle bisector, median and altitude. 

Also, length of altitude of equilateral triangle ie HI and JF = $$\dfrac{\sqrt{3} \times x}{2} $$

Length of diagonal HF = $$\sqrt{2} \times y$$

From the figure, we can express the length of diagonal HF as given : 

$$ \sqrt{2} \times y = \dfrac{\sqrt{3} \times x}{2} + x + \dfrac{\sqrt{3} \times x}{2} $$

$$ \Rightarrow \sqrt{2} \times y = (\sqrt{3} \times x) + x $$

$$ \Rightarrow \sqrt{2} \times y = x \times (\sqrt{3} + 1) $$

$$ \Rightarrow y = x \times (\dfrac{\sqrt{3} + 1}{\sqrt{2}}) $$

Ratio of areas asked = $$(\dfrac{y}{x})^{2} = (\dfrac{\sqrt{3} + 1}{\sqrt{2}})^{2} = \dfrac{4+2\sqrt{3}}{2} = 2+\sqrt{3}$$

Alternate Explanation: 

Let AB=BC=CD=DA=x, then the area the area of square ABCD will be $$x^2$$

Since AHD, DGC, CFB, and BAE are equilateral triangles with side x, the sum of area of these traingles will be $$4\times\ \frac{\sqrt{\ 3}}{4}\times\ x^2=\sqrt{\ 3}x^2$$

We know that angle HAD=60, angle DAB=90, and angle BAE=60, thus angle HAE=360-(60+90+60)=150

Area of triangles HAE+HDG+GCF+FBE=4* area of triangle HAE

In HAE, AH=AE=x, and angle HAE=150, thus area will be $$\frac{1}{2}\times\ x\times\ x\times\ \sin\ 150$$

sin 150=sin(180-150)=sin 30=0.5

Thus area of 4 triangles will be 4*0.5*x*x*0.5=$$x^2$$

Thus, total area= $$x^2+\sqrt{\ 3\ }\ x^2+x^2$$=$$x^2\left(2+\sqrt{\ 3}\right)$$

Thus area of EFGH/area of ABCD=$$2+\sqrt{\ 3}$$