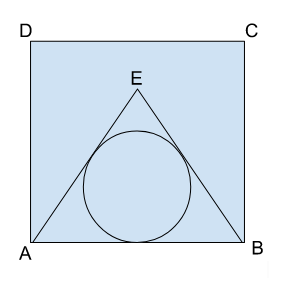
In the given diagram, ABCD is a square of area 300 sq. cm. If triangle ABE is an equilateral triangle. what is the radius of the circle shown in the figure ?

Let us assume that the radius of the circle is r cm and the side of the triangle ABE is a cm.

Then, side of triangle ABE,

$$\Rightarrow$$ $$r$$ = $$\frac{\triangle}{S}$$   (Where $$\triangle$$ = Area of triangle and S = semi-perimeter of triangle)

$$\Rightarrow$$ $$r = \frac{(\frac{\sqrt{3}}{4})\times a^2}{\frac{3a}{2}}$$ 

$$\Rightarrow$$ $$r = \frac{a}{2\sqrt{3}}$$ 

$$\Rightarrow$$ $$a = 2\sqrt{3}\times r$$ 

We are given that the area of square ABCD = 300 sq. cm.

$$\Rightarrow$$    $$a^2 = (2\sqrt{3}\times r)^2$$

$$\Rightarrow$$    $$300 = 12r^2$$

$$\Rightarrow$$    $$r = 5 cm$$

Hence, option C is the correct answer.