Solution
Number of two-digit numbers divisible by 5 = 10, 15, 20,......95
Number of two-digit numbers divisible by 7 = 14, 21, 28,.....98
Number of two-digit numbers divisible by 35 = 35, 70
Using $$S_{n}=\ \dfrac{n}{2}\left(2a+\left(n-1\right)d\right)$$
Sum of the numbers divisible by 5 $$=\dfrac{18}{2}\left(10+95\right)=9\times105=945$$
Sum of the numbers divisible by 7 $$=\dfrac{13}{2}\left(14+98\right)=13\times56=728$$
We need to subtract the numbers divisible by both 5 and 7 $$=35+70=105$$.
So total $$=945+728-105=1568$$
Video Solution
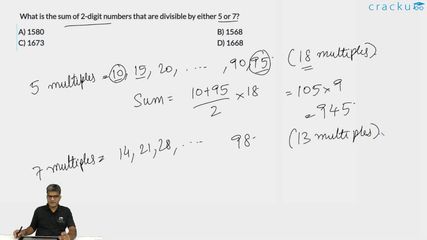
Click on the Email ☝️ to Watch the Video Solution
Create a FREE account and get:
- All Quant Formulas and shortcuts PDF
- 200+ previous papers with solutions PDF
- Top 5000+ MBA exam Solved Questions for Free
