Six friends - P, Q, R, S, T, and U, not necessarily in the same order are standing in a line, facing north. There are as many people between U and S as there are between R and T. S and T are not neighbors. R sits second to the right of S. U and R are neighbors. T sits at one of the ends. P and Q are not neighbors.
Solution
Given, R sits second to the right of S.
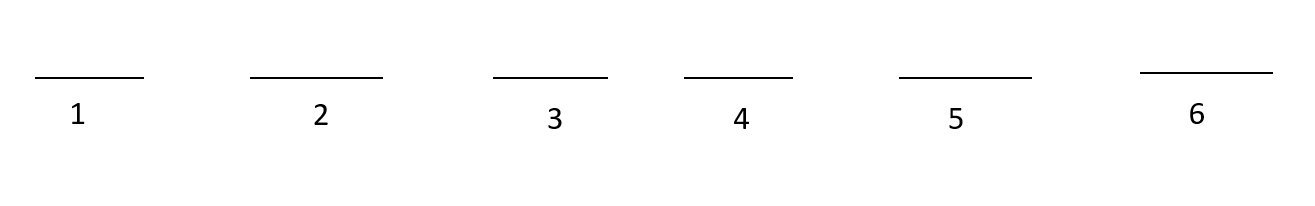
The possible cases are (S, R) are (4, 6), (3, 5), (2, 4) and (1, 3)
If (S, R) sit at (4, 6), U has to sit at 5 as U and R are neighbors. Since the number of people between S and U is same as the number of people between R and T, T has to sit at 3. But T sits at one of the ends, which is not possible.
If (S,R) sit at (3, 5), U can sit at 6 or 4. If U sits at 6, T should sit at 2 as the number of people between S and U is same as the number of people between R and T. This is not possible as T should sit at one of the ends. If U sits at 4, T has to sit at 6. This is not possible as P and Q should not be neighbors.
If (S, R) sit at (2, 4), U can sit 3 or 5. If U sits at 3, T has to sit at 5, which is not possible as T sits at one end. If U sits at 5, T has to sit at 1, but T and S are not neighbors, hence this case is not possible.
If (S, R) sit at (1, 3), U can sit at 2 or 4. U cannot sit at 2 because then T has to sit at 4, which is not possible. If U sits at 4, T has to sit at 6. P, Q can sit at either 2 or 5 in any order.
Thus, 2 cases are possible:
Case 1:

Case 2:
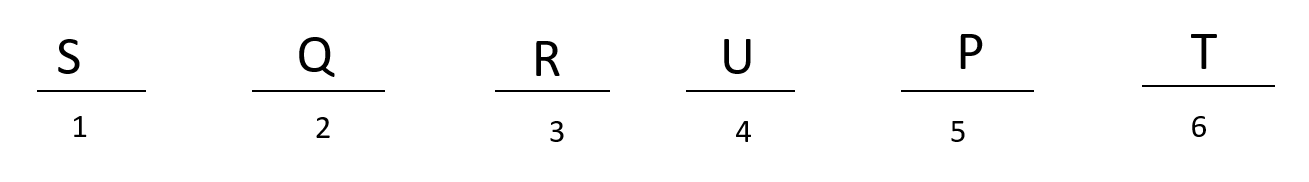
Create a FREE account and get:
- All Quant Formulas and shortcuts PDF
- 200+ previous papers with solutions PDF
- Top 5000+ MBA exam Solved Questions for Free
