Question 18
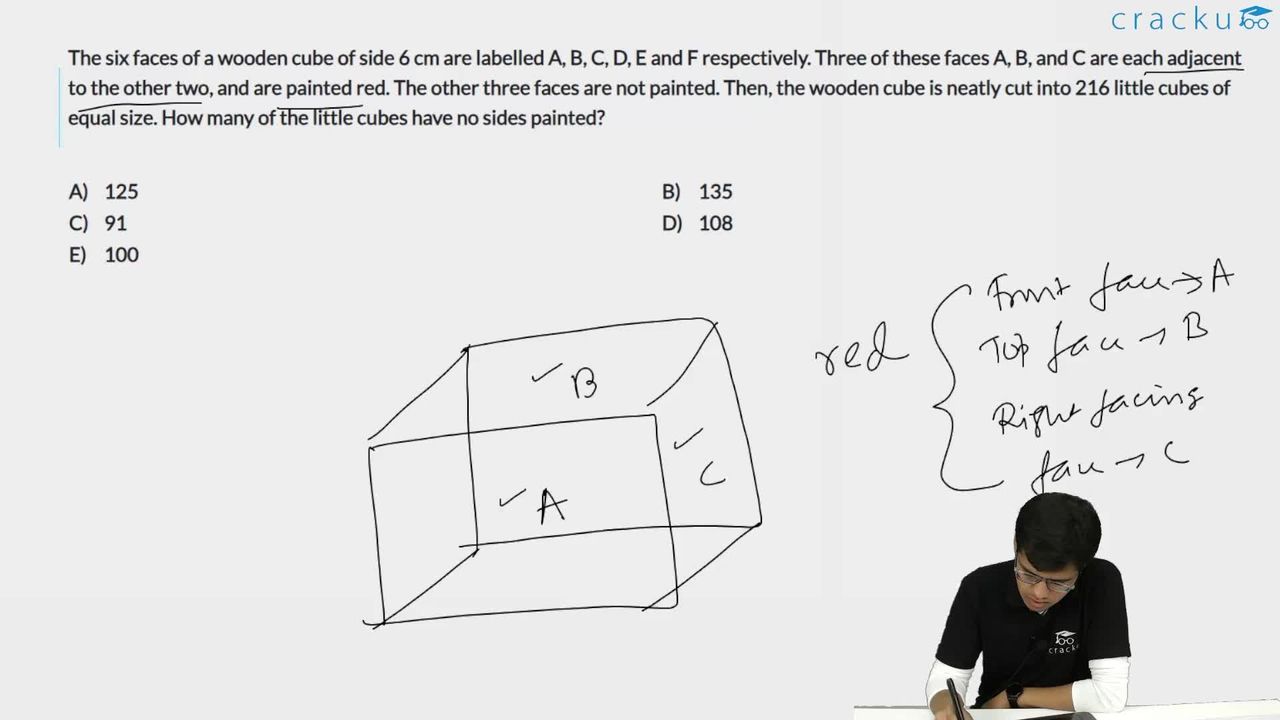
The six faces of a wooden cube of side 6 cm are labelled A, B, C, D, E and F respectively. Three of these faces A, B, and C are each adjacent to the other two, and are painted red. The other three faces are not painted. Then, the wooden cube is neatly cut into 216 little cubes of equal size. How many of the little cubes have no sides painted?
Solution
Since A, B and C are adjacent faces. If we remove them, the resultant solid will also be a cube with side 5.
Hence total number of cubes unpainted = $$5^3$$ = 125
Get AI Help
Video Solution
Click on the Email ☝️ to Watch the Video Solution
XAT Quant Questions | XAT Quantitative Ability
XAT Venn Diagrams QuestionsXAT Progressions and Series QuestionsXAT Functions, Graphs and Statistics QuestionsXAT Time, Speed and Distance QuestionsXAT Inequalities Questions
XAT DILR Questions | LRDI Questions For XAT
XAT Quant Based LR QuestionsXAT DI with connected data sets QuestionsXAT Scheduling QuestionsXAT Data change over a period QuestionsXAT Data Interpretation Questions
XAT Verbal Ability Questions | VARC Questions For XAT
Free XAT Quant Questions
XAT Number SystemsXAT Probability, CombinatoricsXAT InequalitiesXAT Linear EquationsXAT Averages, Ratio and ProportionXAT Venn DiagramsXAT Time, Speed and DistanceXAT Data SufficiencyXAT Functions, Graphs and StatisticsXAT Profit and LossXAT Logarithms, Surds and IndicesXAT GeometryXAT Quadratic EquationsXAT Progressions and Series
