In the given figure, 0 is the centre of the circle and ∠DCE = 45°. If CD = $$10\sqrt2$$ cm, then what is the length (in cm) of AC . CB = BD
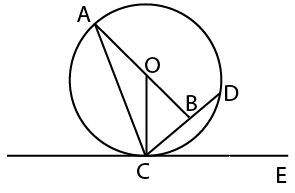
Solution
Given : CD = $$10\sqrt2$$ cm and BC = BD = $5\sqrt2$$
=> ∠OBC = 90°
Also, ∠DCE = 45°, => ∠OCB = 45°, => OB = BC ---------(i)
Now, in $$\triangle$$ OBC,
=> $$(OC)^2=(OB)^2+(BC)^2$$
=> $$(OC)^2=(5\sqrt2)^2+(5\sqrt2)^2$$
=> $$(OC)^2=50+50=100$$
=> $$OC=\sqrt{100}=10$$ cm
Similarly, in $$\triangle$$ ABC,
=> $$(AC)^2=(AB)^2+(BC)^2$$
=> $$(AC)^2=(10+5\sqrt2)^2+(5\sqrt2)^2$$
=> $$(AC)^2=100+50+100\sqrt2+50$$
=> $$(AC)^2=100(2+\sqrt2)=341.42$$
=> $$AC=\sqrt{341.42}=18.47\approx18.5$$ cm
=> Ans - (C)
Create a FREE account and get:
- Free SSC Study Material - 18000 Questions
- 230+ SSC previous papers with solutions PDF
- 100+ SSC Online Tests for Free

