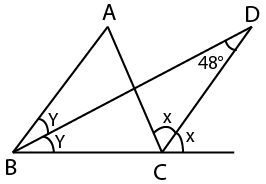
In the given figure, ABC is a triangle. The bisectors of internal ∠B and external ∠C interest at D. If ∠BDC = 48°, then what is the value (in degrees) of ∠A? 

Let $$\angle$$ A = $$\theta$$

Using exterior angle property,

=> $$\theta+2y=2x$$

=> $$2(x-y)=\theta$$

=> $$x-y=\frac{\theta}{2}$$ ------------(i)

In $$\triangle$$ ABC,

=> ∠A + ∠B + ∠C = 180

=> $$\theta+2y+\angle ACB=180^\circ$$

=> $$\angle ACB = 180^\circ-2y-\theta$$

Thus, ∠DCB = ∠ACB + ∠ACD = $$180^\circ-2y-\theta+x$$ -----------(ii)

Now, in $$\triangle$$ BCD,

=> ∠DBC + ∠DCB + ∠CDB = 180

=> $$y+(180^\circ-2y-\theta+x)+48^\circ=180^\circ$$

=> $$x-y-\theta=-48^\circ$$

Substituting value from equation (i), we get :

=> $$\frac{\theta}{2}-\theta=-48^\circ$$

=> $$\frac{\theta}{2}=48^\circ$$

=> $$\theta=48\times2=96^\circ$$

=> Ans - (B)