A cone of diameter of 28cm and height of 48cm is cut horizontally at the height of 24cm from the bottom, and the small cone obtained is attached to the other part in such a way that the centre of the base of the smaller cone touches the centre of the base of the frustum formed of the bigger cone. What is the total surface area of the figure formed?
(take $$\pi$$ as $$\dfrac{22}{7}$$)
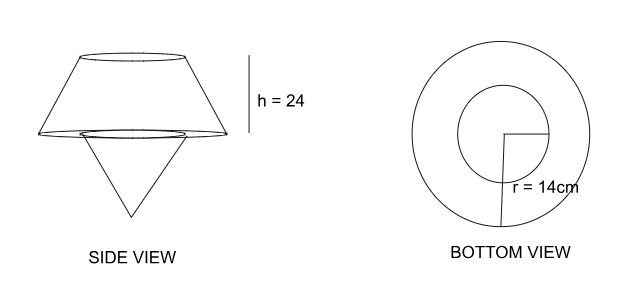
Solution
The total surface area of the bigger cone and the figure formed will be the same as the area in which the smaller cone closes on the base, the same as the area at the top of the other part. So, the total surface area of the figure can be calculated as,
Slant height l = $$\sqrt{\ r^2\ +\ h^2\ }\ =\ \sqrt{\ 14^2\ +\ 48^2}\ =\ \sqrt{\ 2500}\ =\ 50\ $$
Total surface area = $$\pi\ r\left(r\ +\ l\right)$$ = $$\dfrac{22}{7}\ \times\ 14\left(50\ +\ 14\right)\ $$ = $$22\ \times\ 2\ \times\ 64\ $$ = 2816
The correct answer is option D.
