PA and PB are the tangents to a circle with centre O, from a point P outside the circle. A and B are the points on the circle. If $$\angle$$APB = 72$$^\circ$$, then $$\angle$$OAB is equal to:

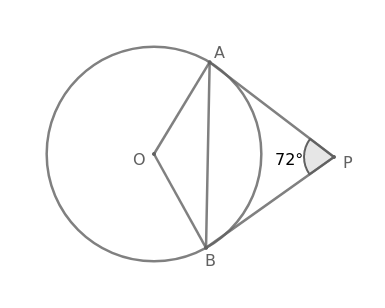
Given,  $$\angle$$APB = 72$$^\circ$$

PA and PB are the tangents to the circle with centre O

$$=$$>  $$\angle$$OAP = 90$$^\circ$$ and  $$\angle$$OBP = 90$$^\circ$$

In quadrilateral OAPB,

$$\angle$$AOB + $$\angle$$OBP + $$\angle$$APB + $$\angle$$OAP = 360$$^\circ$$

$$=$$>  $$\angle$$AOB + 90$$^\circ$$ + 72$$^\circ$$ + 90$$^\circ$$ = 360$$^\circ$$

$$=$$>  $$\angle$$AOB + 252$$^\circ$$ = 360$$^\circ$$

$$=$$>  $$\angle$$AOB = 108$$^\circ$$

In $$\triangle\ $$OAB, OA = OB

Angles opposite to equal sides are equal in triangle

$$=$$>  $$\angle$$OBA = $$\angle$$OAB

In $$\triangle\ $$OAB,

$$\angle$$AOB + $$\angle$$OBA + $$\angle$$OAB = 180$$^\circ$$

$$=$$>  108$$^\circ$$ + $$\angle$$OAB + $$\angle$$OAB = 180$$^\circ$$

$$=$$>   2$$\angle$$OAB = 72$$^\circ$$

$$=$$>   $$\angle$$OAB = 36$$^\circ$$

Hence, the correct answer is Option C