Two points P and Q are at the distance of x and y (where y > x) respectively from the base of a building and on a straight line. If the angles of elevation of the top of the building from points P and Q are complementary, then what is the height of the building?
Solution
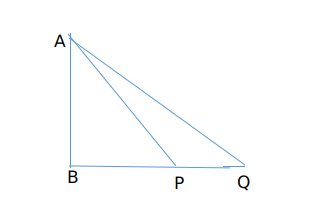
BP =x and BQ=y
AB =h
Now Tan p =h/x (1)
Tan Q=h/y (2)
Now Q=90-P
So Tan Q = Cot P = 1/Tan P
So we get h/x =y/h
we get h^2 =xy
h = $$\sqrt{\ xy}$$
Create a FREE account and get:
- Free SSC Study Material - 18000 Questions
- 230+ SSC previous papers with solutions PDF
- 100+ SSC Online Tests for Free

