Question 5

The two chords AB and CD of a circle intersect at point P, such that BP=4 cm, PD=5 cm, and CP=8 cm. ﬁnd the length of chord AB.

Solution

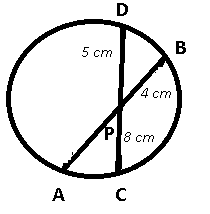
Given : AB and CD are chords of the circle which intersect at point P. BP = 4 cm, CP = 8 cm and PD = 5 cm

To find : AB = ?

Solution : Let AP = $$x$$ cm

Now, when two chords intersect each other inside a circle, the products of their segments are equal.

=> $$(AP)\times(BP)=(CP)\times(DP)$$

=> $$x\times4=8\times5$$

=> $$x=\frac{40}{4}=10$$

$$\therefore$$ AB = AP + PB = $$10+4=14$$ cm

=> Ans - (D)

Create a FREE account and get:

CAT Quant Questions | CAT Quantitative Ability