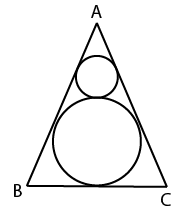
In the given figure. ABC is an equilateral triangle. If the area of bigger circle is 1386 $$cm^2$$. then what is the area $$(in cm^2)$$ of smaller circle? 

Let 'a' be the side of the equilateral triangle then the radius of bigger circle = $$\dfrac{1}{3}\times \dfrac{\sqrt{3}a}{2}$$ = $$\dfrac{a}{2\sqrt{3}}$$

Also the radius of smaller circle = $$\dfrac{1}{3}\times \dfrac{\sqrt{3}a}{6}$$ = $$\dfrac{a}{6\sqrt{3}}$$

We can see that ratio of radius of smaller to larger circle is 1 : 3. Hence, the ratio of the area of smaller to larger circle = 1 : 9

Therefore, the area of the smaller circle = $$\dfrac{1386}{9}$$ = 154 $$cm^2$$