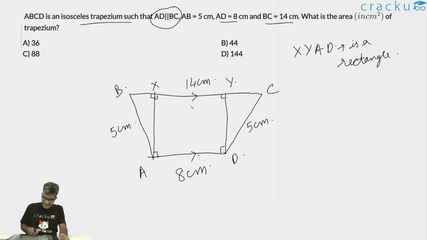
ABCD is an isosceles trapezium such that AD||BC, AB = 5 cm, AD = 8 cm and BC = 14 cm. What is the area $$(in cm^2)$$ of trapezium?

Given : ABCD is an isosceles trapezium and AB = 5 cm, AD = 8 cm and BC = 14 cm

To find : ar(ABCD) = ?

Solution : In an isosceles trapezium AB = CD and BE = CF

Also, AD = EF = 8 cm

=> BE + CF = 14 - 8 = 6 cm

=> BE = CF = $$\frac{6}{2}=3$$ cm

In $$\triangle$$ ABE,

=> $$(AE)^2=(AB)^2-(BE)^2$$

=> $$(AE)^2=(5)^2-(3)^2$$

=> $$(AE)^2=25-9=16$$

=> $$AE=\sqrt{16}=4$$ cm

$$\therefore$$ ar(ABCD) = $$\frac{1}{2}\times (AD+BC)\times(AE)$$

= $$\frac{1}{2}\times(8+14)\times4$$

= $$22\times2=44$$ $$cm^2$$

=> Ans - (B)