Question 41

A ladder 25 metres long is placed against a wall with its foot 7 metres away from the foot of the wall. How far should the foot be drawn out so that the top of the ladder may come down by half the distance of the total distance if the foot is drawn out?

Solution

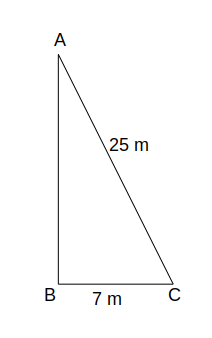
Distance between the top of ladder and foot of wall = $$\sqrt{25^2 - 7^2}$$ = 24 m. Let us assume that C is moved by a distance x m.

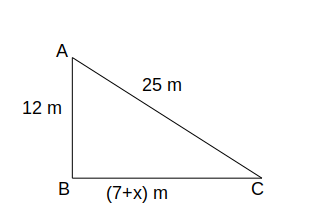
Using, Pythagoras theorem we can say that, 25^2 = 12^2 + (7+x)^2 => x = $$\sqrt{481}$$ - 7 = 14.93 m.

Create a FREE account and get:

All Quant Formulas and shortcuts PDF
40+ previous papers with solutions PDF
Top 500 MBA exam Solved Questions for Free

CAT Quant Questions | CAT Quantitative Ability

CAT Probability, Combinatorics Questions CAT Data Sufficiency Questions CAT Averages, Ratio and Proportion Questions CAT Quadratic Equations Questions CAT Time Speed Distance Questions

CAT DILR Questions | LRDI Questions For CAT

CAT Games and Tournamnents Questions CAT Quant Based DI Questions CAT Truth Lie Concept Questions CAT Puzzles Questions CAT Data Interpretation Basics Questions

CAT Verbal Ability Questions | VARC Questions For CAT

CAT Critical Reasoning Questions CAT Para Summary Questions CAT Miscellaneous Questions CAT Vocabulary Questions CAT Para Jumbles Questions

Follow us on

Boost your Prep!

Download App