Question 37

In the quadrilateral $$ABCD$$ below, $$\angle DAB$$ = 90° and $$AB = 24$$cm , $$BC = 40$$cm, $$CD = 50$$cm and $$AD = 18$$cm(The diagram is not drawn to scale) Find the area of the quadrilateral 

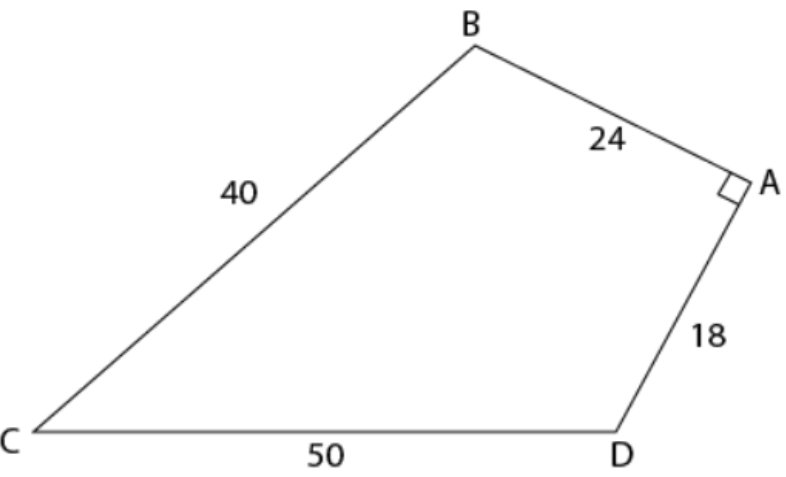
image

Solution

Share
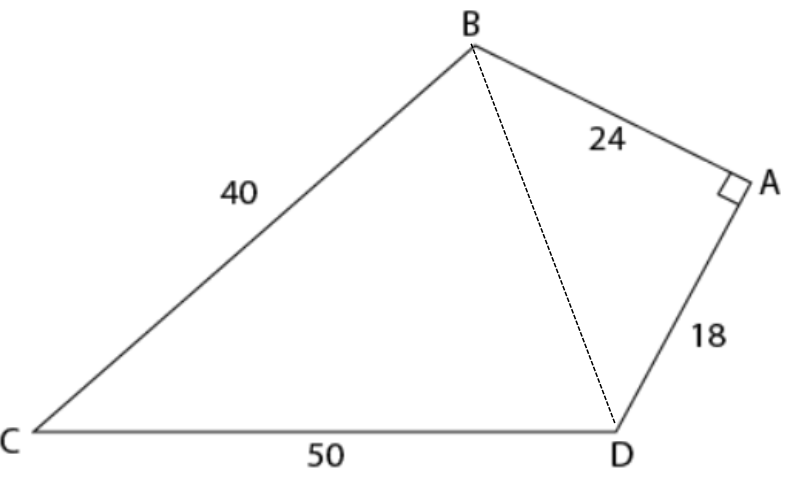
image


Join BD

Area of ABCD = area of ABD + area of BCD

In ABD $$AB^2\ +\ AD^2\ =BD^2$$

Therefore   $$24^{2\ }+\ 18^{2\ }=\ BD^2$$ , on solving BD= 30

also $$30^{2\ }+\ 40^2\ =50^2$$ which implies BCD is also a right-angled triangle, right angled at B. 

Area of ABD = $$\dfrac{1}{2}\times\ 24\times\ 18$$ = 216

Area of BCD = $$\dfrac{1}{2}\times\ 30\times\ 40$$= 600

Area of ABCD = 816

Get AI Help

View More Questions From Geometry

Create a FREE account and get:

  • All Quant Formulas and shortcuts PDF
  • 40+ previous papers with solutions PDF
  • Top 500 MBA exam Solved Questions for Free

PGDBA Quant Questions | PGDBA Quantitative Ability

PGDBA Number Series QuestionsPGDBA Geometry QuestionsPGDBA Simple Interest Compound Interest QuestionsPGDBA Progressions and Series QuestionsPGDBA Time Speed Distance QuestionsPGDBA Miscellaneous QuestionsPGDBA Algebra QuestionsPGDBA Probability, Combinatorics QuestionsPGDBA Inequalities QuestionsPGDBA Percentages QuestionsPGDBA Mensuration QuestionsPGDBA Functions, Graphs and Statistics QuestionsPGDBA Averages QuestionsPGDBA Time, Speed and Distance QuestionsPGDBA Profit and Loss QuestionsPGDBA Time And Work QuestionsPGDBA Data Sufficiency QuestionsPGDBA Coordinate Geometry QuestionsPGDBA Number Systems QuestionsPGDBA Remainders QuestionsPGDBA Profit And Loss QuestionsPGDBA Averages, Ratio and Proportion QuestionsPGDBA Venn Diagrams QuestionsPGDBA Arithmetic QuestionsPGDBA Logarithms QuestionsPGDBA Linear Equations QuestionsPGDBA Logarithms, Surds and Indices QuestionsPGDBA Quadratic Equations QuestionsPGDBA Averages Mixtures Alligations Questions

PGDBA DILR Questions | LRDI Questions For PGDBA

PGDBA Routes And Networks QuestionsPGDBA Charts QuestionsPGDBA Coins and Weights QuestionsPGDBA Quant Based LR QuestionsPGDBA Venn Diagrams QuestionsPGDBA Arrangement QuestionsPGDBA Selection With Condition QuestionsPGDBA Games and Tournaments QuestionsPGDBA Puzzles QuestionsPGDBA Data change over a period QuestionsPGDBA Miscellaneous LR QuestionsPGDBA DI Miscellaneous QuestionsPGDBA Scheduling QuestionsPGDBA Table based DI Sets QuestionsPGDBA Maxima-Minima QuestionsPGDBA DI with connected data sets QuestionsPGDBA Data Interpretation QuestionsPGDBA 2D & 3D LR QuestionsPGDBA Quant Based DI QuestionsPGDBA Data Interpretation Basics QuestionsPGDBA Truth Lie Concept QuestionsPGDBA Special Charts Questions

PGDBA Verbal Ability Questions | VARC Questions For PGDBA

PGDBA Critical Reasoning QuestionsPGDBA Para Jumbles QuestionsPGDBA Para Summary QuestionsPGDBA Reading Comprehension QuestionsPGDBA Verbal Ability QuestionsPGDBA Grammar and Sentence Correction QuestionsPGDBA Vocabulary QuestionsPGDBA Odd One Out Questions

Free PGDBA Topicwise Questions

PGDBA DI with connected data setsPGDBA Functions, Graphs and StatisticsPGDBA Verbal AbilityPGDBA InequalitiesPGDBA Quant Based DIPGDBA Data Interpretation BasicsPGDBA Number SystemsPGDBA Data change over a periodPGDBA AveragesPGDBA Table based DI SetsPGDBA Time And WorkPGDBA Coordinate GeometryPGDBA ChartsPGDBA Selection With ConditionPGDBA Progressions and SeriesPGDBA PuzzlesPGDBA Simple Interest Compound InterestPGDBA Probability, CombinatoricsPGDBA RemaindersPGDBA VocabularyPGDBA Profit and LossPGDBA PercentagesPGDBA Miscellaneous LRPGDBA Linear EquationsPGDBA Quant Based LRPGDBA Logarithms, Surds and IndicesPGDBA Data InterpretationPGDBA ArrangementPGDBA Critical ReasoningPGDBA Odd One OutPGDBA Ssc ReasoningPGDBA Number SeriesPGDBA Routes And NetworksPGDBA MiscellaneousPGDBA Averages, Ratio and ProportionPGDBA Data SufficiencyPGDBA Quadratic EquationsPGDBA MensurationPGDBA Venn DiagramsPGDBA Coins and WeightsPGDBA AlgebraPGDBA Time, Speed and DistancePGDBA ArithmeticPGDBA Games and TournamentsPGDBA SchedulingPGDBA Para JumblesPGDBA Venn DiagramsPGDBA LogarithmsPGDBA Time Speed DistancePGDBA 2D & 3D LRPGDBA Reading ComprehensionPGDBA Grammar and Sentence CorrectionPGDBA Averages Mixtures AlligationsPGDBA DI MiscellaneousPGDBA Special ChartsPGDBA Maxima-MinimaPGDBA Truth Lie ConceptPGDBA GeometryPGDBA Profit And LossPGDBA Para Summary

Book Free CAT Mentorship

Get personalized CAT strategy from a 99%iler

500+ students mentored
CAT mentor

Join CAT 2026 course by 5-Time CAT 100%iler

Start your IIM journey with the right preparation and crack CAT 2026.

Enroll Now
Ask AI