In the given figure. $$ABCDEF$$ is a regular hexagon whose side is 6 cm. $$APF, QAB, DCR$$ and $$DES$$ are equilateral triangles. What is the area (in $$cm^2$$) of the shaded region?

We have :

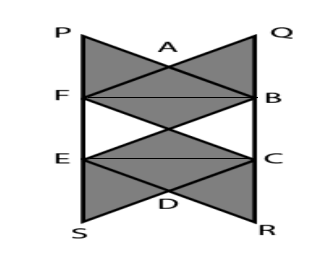
We here have 6 equilateral triangles of side 6cm so we can say a complete hexagon and half area of rectangle BCFE
Now In triangle ABF
using cosine rule
we get cos A = (6^2+6^2-BF^2)/2AF AB
we get BF $$6\sqrt{\ 3}$$
Area of shaded region = Area of hexagon + 0.5(Area of rectangle BFCE)
we get area = $$6\times\ \frac{\sqrt{\ 3}}{4}\times\ 6\times\ 6\ +\ 6\sqrt{\ 3}\times\ 6\times\ 0.5$$
= $$54\sqrt{\ 3}+18\sqrt{\ 3}\ =72\sqrt{\ 3}$$