A man covers a distance of 1200km in 70 days resting 9 hours a day. If he rests 10 hours a day and walks with speed $$1\frac{1}{2}$$ times the previous speed, then in how many days will he cover 840km?

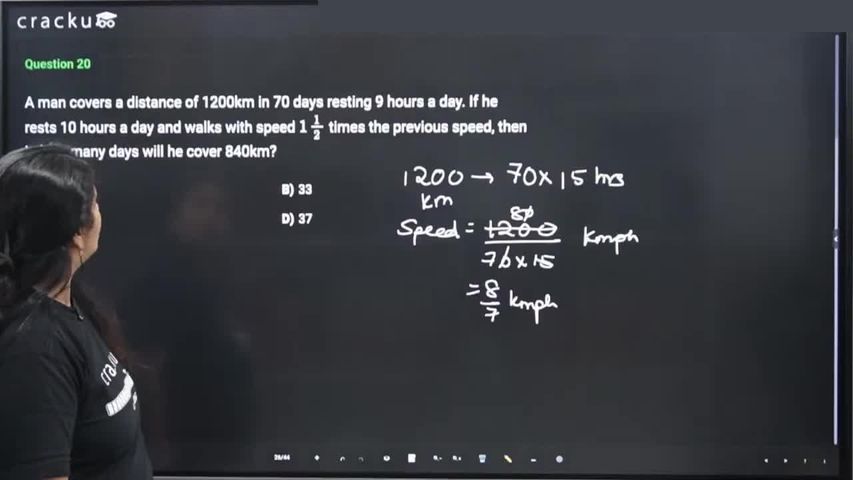
In a day of 24 hours, if the person is taking 9 hours of rest, then he is walking for 24 - 9 = 15 hours a day. 

The number of hours he walks in 70 days is 70 * 15 = 1050 hours.

Speed of the person = $$\dfrac{1200}{1050}\ =\ \dfrac{8}{7}$$ kmph

If he increases his speed by $$1\dfrac{1}{2}\ =\ \dfrac{3}{2}$$ times, the speed becomes $$\dfrac{8}{7}\ \times\ \dfrac{3}{2}\ =\ \dfrac{12}{7}$$ kmph.

If he is covering 840 km, the time taken to cover the distance is $$\dfrac{840}{\frac{12}{7}}\ =\ 840\ \times\ \dfrac{7}{12}\ =\ 490$$ hours.

In a day, if he takes 10 hours of rest, then he is walking for 24 - 10 = 14 hours a day.

Total number of days taken by the person  = $$\dfrac{490}{14}\ =\ 35$$ days.

Hence, the correct answer is option C.