Please enter the following details
Read the information given below and answer the 2 associated questions.
190 students have to choose at least one elective and at most two electives from a list of three electives: E1, E2 and E3. It is found that the number of students choosing E1 is half the number of students choosing E2, and one third the number of students choosing E3.
Moreover, the number of students choosing two electives is 50.
Given, a+b+c=50 and a+b+c+x+y+z=190 => x+y+z=140.
Also, let E1=k => E2=2k and E3=3k
E1+E2+E3= 6k=190+50=240 => k=40.
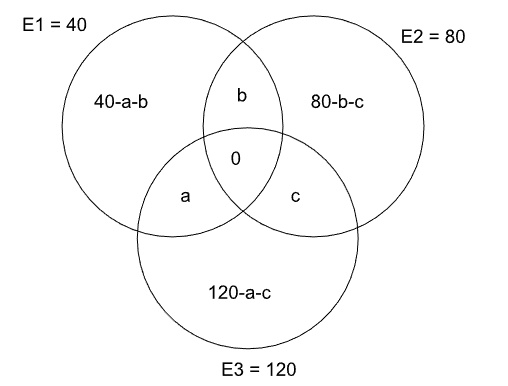
Option A, the number of students choosing E1 is 40.
Option B, number of students choosing either E1 or E2 or both, but not E3 = total - E3 = 190-120 = 70.
Option C, number of students choosing both E1 and E2 => this can not be obtained.
Option D, number of students choosing E3 = 3x = 120.
Option E, number of students choosing exactly one elective = Out of 190, 50 are choosing two electives, hence 190-50 = 140 are choosing exactly one elective.
