Please enter the following details
Free Daily Targets & Mocks
Study Material & Formulas PDFs
1 on 1 Mentorship
Question 20
A man walks 20 m towards north, then he turns right and walks 3 m, then turns left and walks 4 m and from there he walks 4 m towards east. How far and in which direction is he from his initial position?
Solution
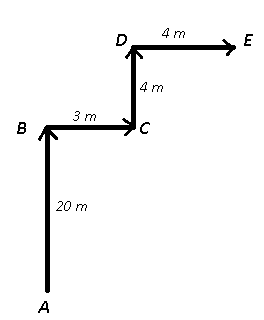
Let the man starts from point A and walked 20 m north to reach point B, then he turned right towards east and walked for 3 m, from point C he turned left to reach D after walking 4 m and finally stopped at point E.
Thus, AE = $$\sqrt{(20+4)^2+(4+3)^2}$$
=> $$AE=\sqrt{576+49}=\sqrt{625}$$
=> $$AE=25$$ m
Thus, he is 25 m north-east of his original position.
=> Ans - (B)
Video Solution
Create a FREE account and get:
- Free SSC Study Material - 18000 Questions
- 230+ SSC previous papers with solutions PDF
- 100+ SSC Online Tests for Free
