The cliff of a mountain is 180 m high and the angles of depression of two ships on the either side of cliff are $$30^{0}$$ and $$60^{0}$$. What is the distance between the two ships ?

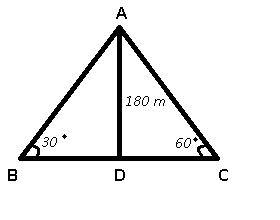
Given : AD is the mountain = 180 m

To find : Distance between the ships = BC = ?

Solution : In $$\triangle$$ ADC

=> $$tan(60^\circ)=\frac{AD}{DC}$$

=> $$\sqrt{3}=\frac{180}{DC}$$

=> $$DC=\frac{180}{\sqrt{3}}$$ m

Similarly, in $$\triangle$$ ABD

=> $$tan(30^\circ)=\frac{AD}{BD}$$

=> $$\frac{1}{\sqrt3}=\frac{180}{BD}$$

=> $$BD=180\sqrt3$$ m

$$\therefore$$ BC = BD + DC

= $$(180\sqrt3 + \frac{180}{\sqrt{3}})$$

= $$\frac{540+180}{\sqrt3}=\frac{720}{\sqrt3}$$

= $$240\sqrt3=240\times1.732=415.68$$ m

=> Ans - (C)